Question about order statistics of Uniform distribution

Question

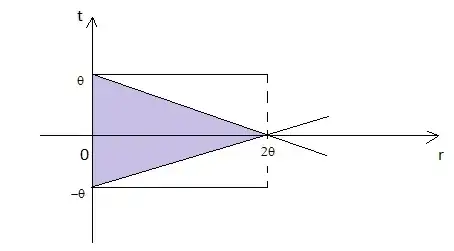
Let $X_i$ be i.i.d $\operatorname{Uniform}(-\theta,\theta)$ random variables, and let $X_{(1)},\dotsb, X_{(n)}$ the order statistics of the random variables. Then find distribution of $Y = X_{(n)} - X_{(1)}$.

I used pdf of order statistics to solve this problem.

we know pdf of $(X_{(r)},X_{(s)})^t$ $(1 \leq r<s \leq n)$ is

$f_{X_{(r)},X_{(s)}} (x,y) = {n! \over {(r-1)!(s-1-r)! (n-s)!}}[F(x)]^{r-1}[F(y)-F(x)]^{s-1-r}[1-F(y)]^{n-s}f(x)f(y)$

So, $f_{X_{(1)},X_{(n)}}(x_1,x_n) = {n! \over {(n-2)!}}({x_n - x_1 \over 2\theta})^{n-2}({1 \over 2\theta})^2 I_{(-\theta<x_1<x_n<\theta)}$

Let $X \equiv X_{(1)}$ and $u : \begin{cases}X = X_{(1)}\\Y = X_{(n)} - X_{(1)}\end{cases}$, $u^{-1} :\begin{cases}x_{(1)} = x\\x_{(n)} = x+y\end{cases}$ , $u$ : one to one , $\Bigl\lvert \det\Bigl( {\partial(x_{(1)},x_{(n)}) \over {\partial (x,y)}}\Bigr) \Bigr\rvert = 1$

$\therefore f_{X,Y}(x,y) =f_{X_{(1)},X_{(n)}}(x_1,x_n)\Bigl\lvert \det\Bigl( {\partial(x_{(1)},x_{(n)}) \over {\partial (x,y)}}\Bigr) \Bigr\rvert = n(n-1)y^{n-2}({1 \over 2\theta})^n I_{(-\theta,\theta-y)}(x) I_{(-\theta,\theta)}(y)$

$\therefore f_Y(y) = \int_{-\theta}^{\theta-y} f_{X,Y}(x,y)\, dx = n(n-1)y^{n-2}({1 \over 2\theta})^n (2\theta - y) I_{(0,1)}(y)$

I can't find answer of this problem. Can you help me please?

Answer 1

The fastest way to proceed is to observe that the joint density $(R;T)$, that is the joint density Range - Midrange is known and, after some simple algebraic calculations, you get:

$$f_{RT}(r,t)=\frac{n(n-1)}{2^n\cdot \theta^n}r^{n-2}$$

Thus you can find the marginal $f_R(r)$ integrating in $dt$

The remaining problem is to identify correctly the joint and marginal support to find the correct integral bounds...

after some calculations I got

$$ \bbox[5px,border:2px solid black] { f_R(r)=\frac{n(n-1)}{(2\theta)^n}r^{n-2}(2\theta-r)\cdot\mathbb{1}_{(0;2\theta)}(r) \ } $$

which is the same as yours but with a different support.

Here is an example with $n=5$ and $\theta=1$

Answer 2

If you don't mind, can you explain how you got the support?

Consider the following system, setting $y>x$

$$\begin{cases} r=y-x\\ t=\frac{x+y}{2} \end{cases} \rightarrow \begin{cases} x=t-\frac{r}{2}\\ y=t+\frac{r}{2} \end{cases}$$

you see that, being $\theta<x<\theta$ and $-\theta<y<\theta$ it results that the joint support $(R;T)$ is

$$\begin{cases} t<\theta-\frac{r}{2}\\ t>\frac{r}{2}-\theta \end{cases} $$

which is the following region

Now you can easy integrate in $dr$ to obtain the density of the midrange or in $dt$ to obtain the density of the range

The marginal supports are, evidently:

$$R\in(0;2\theta)$$

$$T \in(-\theta;\theta)$$