How do I compute the distribution of $\min\{X,Y,1-Y,1-X$ $,|X-Y|,1-|X-Y|\}$, where $X,Y \overset{\text{iid}}{\sim} \operatorname{Unif}(0,1)$?

Question

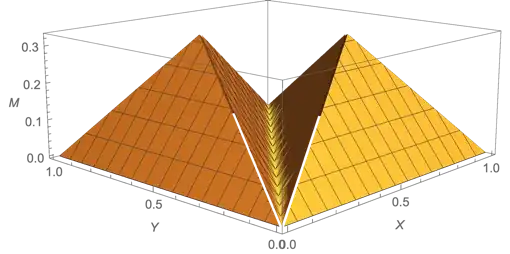
Let $X,Y \overset{\text{iid}}{\sim} \operatorname{Unif}(0,1)$. Let $$M = \min\{X,Y,1-Y,1-X,|X-Y|,1-|X-Y|\}.$$ Supposedly $\operatorname{image}(M) \subseteq (0,\frac13)$ and distribution of $M$ is $$F_M(m)= (3m(2-3m))1_{(0,\frac13)}(m) + 1_{(\frac13,\infty)}(m).$$ See here.

Question: How do I compute the distribution of $M$? I wonder if there's a clever way of doing this like with $W$ here. Below is what I've tried so far.

Well $|X-Y| \ge m$ and $1-|X-Y| \ge m$ tell me $m \le |X-Y| \le 1-m$. So it looks like I have 4 cases

1. $x+(m-1) \le y \le x-m$

2. $x+m \le y$

3. $y \le x-m$

4. $x-(m-1) \le y \le x+m$ (but I think I rule out this last case because here I have $m \ge \frac12$.

Then $X,Y,1-Y,1-X \ge m$ tell me $m \le X \le 1-m$ and $m \le Y \le 1-m$. So I guess the 3 cases become

1. $x+m-1 = \max\{m,x+m-1\} \le y \le \min\{x-m,1-m\} = x-m$

2. $x+m = \max\{m,x+m\} \le y \le 1-m$

3. $m \le y \le \min\{x-m,1-m\} = x-m$

But it seems if I do $\int_0^1 \int_{\cdot}^{\cdot} 1\, dy \,dx$ for each case and then add them up I get only $2-6m$.

Answer 1

As a function of $X$ and $Y$, $M$ has the following symmetries:

$$ \begin{align} M(X,Y)&=M(Y,X), \\ M(X,Y)&=M(1-X,1-Y), \\ M(X,Y)&=M(|X-Y|,\max(X,Y)). \end{align} $$

Being the minimum of piecewise-linear functions, its graph is piecewise-linear (the symmetries can help understand this graph):

Alternatively, here is the corresponding contour plot:

Having found the maximum of $M$ to be $1/3$, we can see that the survival function, $P(M(X,Y)>m)$ is obtained by integrating over 2 congruent right triangles in the uniform $(X,Y)$ space.

Note that the length of a leg of one of these triangles, $l(m)$, satisfies $$l(0)=1, \\l(1/3)=0. $$ Linear interpolation then gives

$$l(m)=1-3m, $$ and thus $$P(M(X,Y)>m) = (1-3m)^2. $$

Finally, the CDF is

$$1-(1-3m)^2 , 0 \leq m \leq 1/3.$$

Answer 2

I'm not sure how defining $H$ is relevant, so I'm going to ignore that part of your question.

We start by observing that if $$M(X,Y) = \min\{X, Y, 1-Y, 1-X, |X-Y|, 1 - |X-Y|\},$$ then $$M(X,Y) = M(Y,X),$$ so we can restrict our attention to the case $0 \le Y \le X \le 1.$, which describes a triangular domain on the unit square. Then on this domain, $$M(X,Y) = \min\{Y, 1-X, X-Y\}.$$ This is because:

• We can eliminate $X$ since $X \ge Y$.
• We can eliminate $1-Y$ because $1-Y \ge 1-X$.
• $|X-Y| = X-Y$ since $X \ge Y$.
• $1-|X-Y| = 1-X+Y \ge 1-X$, so we can eliminate this also.

Consequently, the probability $$\Pr[M > m \mid 0 \le Y \le X \le 1] \\ = \Pr[(Y > m) \cap (1-X > m) \cap (X-Y > m) \mid 0 \le Y \le X \le 1], \tag{1}$$ since in order for $M > m$, each of $Y, 1-X, X-Y$ must exceed $m$; conversely, if each of $Y, 1-X, X-Y$ exceed $m$, then $M > m$. But the simultaneous inequalities on the RHS of $(1)$ can be interpreted as the region of the $(X,Y)$-plane comprising the interior of an isosceles triangle with vertices at $$(2m,m), (1-m, m), (1-m, 1-2m).$$ The first vertex comes from combining the first and last inequality: $Y > m$ and $X - Y > m$ implies $X > m + Y > 2m$. The second vertex is direct from the first and second inequalities. And the third vertex comes from the second and third inequalities: $X < 1-m$ and $Y < X-m$ implies $Y < 1-2m$. So, remembering the symmetry about $X = Y$, the desired probability is equal to twice the area of this triangle, namely $$\Pr[M > m] = \begin{cases} 1, & m < 0 \\ (1 - 3m)^2, & 0 \le m \le 1/3 \\ 0, & m > 1/3. \end{cases} $$ hence $$f_M(m) = 6(1-3m) \mathbb 1(0 \le m \le 1/3).$$

Answer 3

For any $m\in[0,1]$,

\begin{align} F_M(m)&=1-\mathbb{P}\{M>m\} \\ &= 1-\mathbb{P}\{X\in (m,1],Y\in (m,1],1-Y\in (m,1],1-X\in (m,1],\\ &\hspace{7cm}|X-Y|\in (m,1],1-|X-Y|\in (m,1]\}\\ \\ &= 1- \mathbb{P}\{X\in(m,1-m),Y\in(m,1-m),|X-Y|\in(m,1-m)\}\\ \\ &= 1- \mathbb{P}\{X\in(m,1-m),Y\in(m,1-m),X-Y\in(m,1-m),X\geq Y\}\\ &\hspace{2cm}- \mathbb{P}\{X\in(m,1-m),Y\in(m,1-m),Y-X\in(m,1-m),X < Y\}\\ \\ &= 1-2\mathbb{P}\{X\in(m,1-m),Y\in(m,1-m),X-Y\in(m,1-m),X\geq Y\}\\ \\ &= 1-\begin{cases} 2\mathbb{P}\{Y\in(m,1-2m),X\in(m+Y,1-m)\} & \text{ if } m<1-2m \\ 0 & \text{ if } m\geq 1-2m \end{cases}\\ \\ &= \begin{cases} 1-2\int_{y=m}^{1-2m}\int_{x=m+y}^{1-m} 1\cdot dxdy=6m-9m^2 & \text{ if } 0\leq m<1/3 \\ 1 & \text{ if } m\geq 1/3. \end{cases}\\ &= 3m(2-3m)\mathbb{1}_{\left(0,\frac13\right)}(m) + \mathbb{1}_{\left(\frac13,\infty\right)}(m). \end{align}

Answer 4

Ok here's what I did on wolfram:

By trying out values of $m=\frac15, \frac16, \frac17$ (Btw: $\frac14$ was kind of an outlier. See below re 'only issue'. Also, as expected, $\frac13$ gave no solutions), I got 4 cases

1. $x \in (m,2m)$, $y \in (x+m,1-m)$
2. $x \in (2m,1-2m)$, $y \in (m, x-m)$
3. $x \in (2m,1-2m)$, $y \in (x+m, 1-m)$
4. $x \in (1-2m,1-m)$, $y \in (m,x-m)$

When sketching this, I ended up getting 4 trapezoid figures.

Anyhoo, I got

1. $\int_m^{2m} \int_{x+m}^{1-m} 1 dy dx$

2. $\int_{2m}^{1-2m} \int_{m}^{x-m} 1 dy dx$

3. $\int_{2m}^{1-2m} \int_{x+m}^{1-m} 1 dy dx$

4. $\int_{1-2m}^{1-m} \int_{m}^{x-m} 1 dy dx$

5. Combining (1) and (3), we get $\int_m^{1-2m} \int_{x+m}^{1-m} 1 dy dx$

6. Combining (2) and (4), we get $\int_{2m}^{1-m} \int_{x+m}^{1-m} 1 dy dx$

7. Combining (5) and (6) we get our desired distribution.

My one issue however is the very fact that we say $(2m,1-2m)$ in the first place suggests $m \in (0,\frac14)$ only! (See above re 'outlier'.) I mean, I don't think $2m$ and $1-2m$ should be compared, but I think $m$ and $1-m$ should be compared.

I think this can be fixed if we just do 2 cases

1. $x \in (m,1-2m)$, $y \in (x+m,1-m)$, combining (1) and (3)
2. $x \in (2m,1-m)$, $y \in (m, x-m)$, combining (2) and (4)