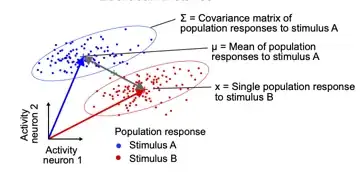
Given that I want to calculate the distance of a vector x (say from the blue distribution) from the centroid of a different distributions than x's - say centroid of the red vectors:
I want to use the Mahalanobis distance:
$M^2 = (x-\mu)^T \Sigma^{-1}(x-\mu)$
Is the covariance matrix $\Sigma^{-1}$ than calculated only from the distribution of the here red vectors? If so, how is the distribution of the blue datapoints considered?