Let $E$ be the $n$-dimensional ellipsoid defined by $$E:=\{x \in \mathbb{R}^n: (x-c)^T A (x-c) \le 1\},$$ where $c \in \mathbb{R}^n$ is the center of the ellipsoid, and $A \in \mathbb{R}^{n \times n}$ is a symmetric positive definite matrix.
Question: How can one efficiently compute the coordinate-axis-aligned bounding box that just barely contains the ellipsoid?
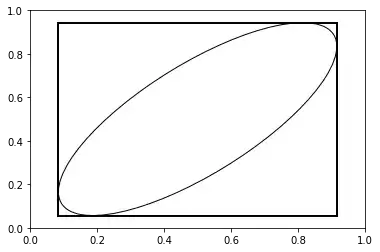
For a 2D example, see the following picture:
Note: I ask this question, and answer it myself, because this question (in general form) is surprisingly absent from math.stackexchange even after 10+ years. Good answers to this question are hard to find on the internet more generally. After googling around, I eventually had to figure this out myself, and am posting here to spare future people the same trouble. Many websites discuss the question in the special case of $2D$ and $3D$, but the the format of the ellipse is given in terms of axes and angles rather than SPD matrices, and the formulas do not generalize to n-dimensions. The good answer is given by achilles hui in the comments to the following closed question: Bounding box of Ellipsoid but no proof is provided there, and the question is closed so I cannot provide the answer with proof there. Even if that question were reopened, it is focused on the 3D case with axes and angles rather than the n-dimensional case with SPD matrices.