Given a rectangle of length 2a and width 2b (assume a$> $b if required). Find an ellipse of maximum area circumscribed by the given rectangle.
You may take rectangle sides parallel to coordinate axis.
I guess ellipse to be $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ because this question is very similar and may be same to (infact may be another way of asking) this but I am not sure.
Let $ABCD$ be the given rectangle, with horizontal and vertical sides. Suppose that an ellipse is inscribed as shown on the left, so that its axes are not parallel to the sides of the rectangle. Points, $P$, $Q$, $R$, and $S$ are the points of tangency. Diameter $KL$ is horizontal.
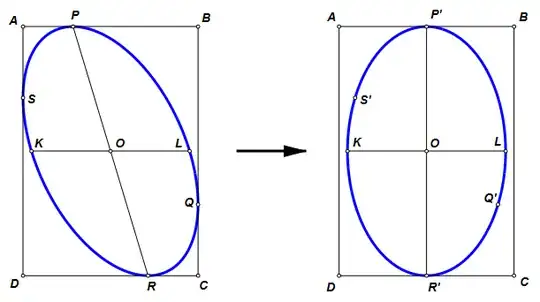
Let a shear transformation be defined such that line $KL$ is invariant and diameter $PR$ is mapped to a vertical line. Let the ellipse be transformed, but not the rectangle.
In the ellipse image, diameter $P'R'$ is now an axis. Diameter $KL$, invariant in the transformation, is the other axis, still shorter than the horizontal dimension of the rectangle. Therefore, the area of this ellipse is less than the greatest area possible.
Areas are conserved in the shear transformation, meaning the pre-image cannot have the maximum possible area. That goes for any inscribed ellipse whose axes are not parallel to the sides of the rectangle. The only alternative, then, is just what you conjectured.
