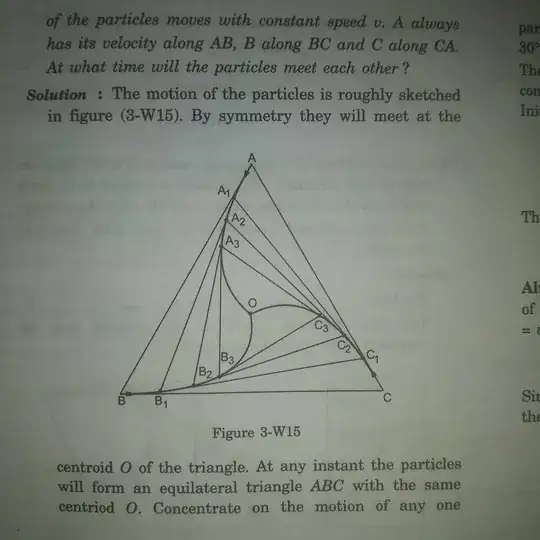
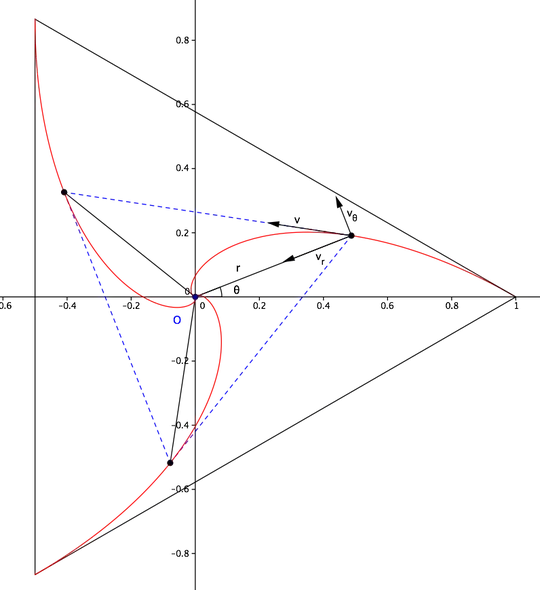
So I just was solving this standard problem when a question struck my mind. What is the nature of this path? I tried my best and all i was able to do was to prove that it is not a circle. Here is the pic:
Basically three particles starts moving with a constant speed from their respective corner of an equilateral triangle such that velocity is one particle is always directed to another. Once again, I am trying to find the nature of the path followed by any particle.
Let's choose a coordinate system with the origin $O$ at the centre of the triangle and with a particle initially at $(1,0)$. At every moment the particles lie at the vertices of an equilateral triangle, their distances $r$ from $O$ being equal and their polar angles $\theta$ differing by $120°$.
Velocity vector $\vec v$ of the first particle is directed towards the second particle: its projection along the radial direction is $v_r=\dot r=-v\cos30°=-(\sqrt3/2)v$, while its projection along the azimuthal direction is $v_\theta=r\dot\theta=v\cos60°=(1/2)v$. It follows that: $$ {dr\over d\theta}={\dot r\over\dot\theta}=-\sqrt3r, $$ which can be solved to yield $$ r=e^{-\sqrt3\theta}. $$ This is the polar equation of a logarithmic spiral.
