3

Could you please help me to find a survival function for Poisson distribution? I'm very new to this topic. Poisson distribution probability mass function:

$$f(k) = P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}.$$

So, I found a general definition of survival function:

$$S(t) = P(T > t) = \int_t^\infty f(u)\,du = 1 - F(t).$$

But as I understand, this one suits only continuous distributions and Poisson is a discrete one. Then I found this definition, which seems to suit a discrete case:

$$S(t_j) = S_j = P(T \geq t_j) = \sum_{k=j}^\infty f(k).$$

But as I wasn't counting it earlier, I'm not sure how to apply it. I need it for my university project. Also, found that this is a survivor function for Poisson: 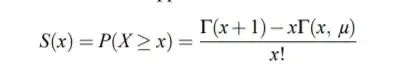enter image description here But don't know how to find it.

Adolf Miszka
  • 480
  • 1
    Do you want the answer - or would you prefer an hint that would help you derive the answer. The first is easier - but the latter is more fun ... your choice. – firdaus Nov 01 '20 at 22:46
  • 2
    Different people define the survival function differently for discrete distributions, either as $\mathbb P(T \gt t)=1-F(t)$ or as $\mathbb P(T \ge t)$ – Henry Nov 01 '20 at 23:55
  • 1
    @firdaus as it's quite urgent for me now, I would like to see a solution if you have it. – Adolf Miszka Nov 02 '20 at 12:35
  • 1
    @Henry thanks for this note. Then I more interested in this definition: $\mathbb P(T \gt t)=1-F(t)$ . – Adolf Miszka Nov 02 '20 at 12:35
  • 1
    @StubbornAtom it seems like something similar, but I don't see anything that it is a survival function, also other markings and task is really different. Maybe, because I'm new to this it doesn't fully answer my question. – Adolf Miszka Nov 02 '20 at 18:18

0 Answers0