Prompted by your wish to see an answer, may I present you with my own. I would like to say that I consider this to be a very straightforward approach, since it relies on nothing else than the definition of the cotangent function in order to establish a more general, purely algebraic version of the identity in question.
Let us recall the definition of the complex exponential:
$$\mathrm{e}^z\colon=\sum_{n=0}^{\infty}\frac{z^n}{n!}$$
and the rigorous definitions of the complex trigonometric functions:
$$\begin{align}
&\sin, \cos \colon \mathbb{C} \to \mathbb{C}\\
&\sin z\colon=\frac{\mathrm{e}^{\mathrm{i}z}-\mathrm{e}^{-\mathrm{i}z}}{2\mathrm{i}}\\
&\cos z\colon=\frac{\mathrm{e}^{\mathrm{i}z}+\mathrm{e}^{-\mathrm{i}z}}{2}\\
&\mathrm{tg}\colon \mathbb{C}\setminus \pi\left(\mathbb{Z}+\frac{1}{2}\right) \to \mathbb{C}\\
&\mathrm{tg}z\colon=\frac{\sin z}{\cos z}\\
&\mathrm{ctg}\colon \mathbb{C}\setminus \pi \mathbb{Z}\to \mathbb{C}\\
&\mathrm{ctg}z\colon=\frac{\cos z}{\sin z}=\frac{1}{\mathrm{tg}z},
\end{align}$$
adding the remark that the definition domains for the tangent and cotangent functions are dictated by the zero-sets of the sine and cosine, namely $\sin^{-1}[\{0\}]=\pi \mathbb{Z}$ and $\cos^{-1}[\{0\}]=\pi\left(\mathbb{Z}+\frac{1}{2}\right)$. Let us also remark that the cotangent admits an explicit description as a rational function of the complex exponential, as follows:
$$\begin{align}
\mathrm{ctg} z&=\frac{\cos z}{\sin z}\\
&=\frac{\frac{\mathrm{e}^{\mathrm{i}z}+\mathrm{e}^{-\mathrm{i}z}}{2}}{\frac{\mathrm{e}^{\mathrm{i}z}-\mathrm{e}^{-\mathrm{i}z}}{2\mathrm{i}}}\\
&=\mathrm{i}\frac{\mathrm{e}^{\mathrm{i}z}+\mathrm{e}^{-\mathrm{i}z}}{\mathrm{e}^{\mathrm{i}z}-\mathrm{e}^{-\mathrm{i}z}}\\
&=\mathrm{i}\frac{\mathrm{e}^{2\mathrm{i}z}+1}{\mathrm{e}^{2\mathrm{i}z}-1}.
\end{align}$$
Let us now consider an arbitrary natural number $n \in \mathbb{N}$ together with a family $u \in \mathbb{C}^n$ of complex numbers such that $\{u_k-u_l\}_{\substack{1 \leqslant k, l \leqslant n\\ k \neq l}} \cap \pi \mathbb{Z}=\varnothing$ and let us study the identity:
$$\sum_{k=1}^n \prod_{\substack{1 \leqslant l \leqslant n\\l \neq k}}\mathrm{ctg}(u_l-u_k)=\sin\frac{n\pi}{2}$$
by substituting all the cotangents with their explicit expressions described above:
$$\sum_{k=1}^n \prod_{\substack{1 \leqslant l \leqslant n\\l \neq k}}\left(\mathrm{i}\frac{\mathrm{e}^{2\mathrm{i}(u_l-u_k)}+1}{\mathrm{e}^{2\mathrm{i}(u_l-u_k)}-1}\right)=\sin \frac{n\pi}{2},$$
which by a suitable amplification of each of the fractions is also equivalent to:
$$\sum_{k=1}^n \mathrm{i}^{n-1}\prod_{\substack{1 \leqslant l \leqslant n\\l \neq k}}\frac{\mathrm{e}^{2\mathrm{i}u_l}+\mathrm{e}^{2\mathrm{i}u_k}}{\mathrm{e}^{2\mathrm{i}u_l}-\mathrm{e}^{2\mathrm{i}u_k}}=\sin \frac{n\pi}{2}$$
and hence eventually to:
$$\sum_{k=1}^n\prod_{\substack{1 \leqslant l \leqslant n\\l \neq k}}\frac{\mathrm{e}^{2\mathrm{i}u_l}+\mathrm{e}^{2\mathrm{i}u_k}}{\mathrm{e}^{2\mathrm{i}u_l}-\mathrm{e}^{2\mathrm{i}u_k}}=(-\mathrm{i})^{n-1}\sin \frac{n\pi}{2}.$$
This final form of the identity in question has the advantage of "separating" the variables, in the more precise sense that the exponentials in $u_l$ respectively $u_k$ vary essentially independently in each of the fractions which occur as factors in the products above (the sole condition to which they are subjected being the one concerning their differences, not allowed to be integer multiples of $\pi$). Taking into account the fact that the right-hand side has the following explicit description:
$$(-\mathrm{i})^{n-1}\sin \frac{n \pi}{2}=\begin{cases}
0, &n \in 2\mathbb{N}\\
1, &n \in 2\mathbb{N}+1,
\end{cases}$$
the above form of our identity suggests the following universal relation:
$$\sum_{k=1}^n\prod_{\substack{1 \leqslant l \leqslant n\\ l \neq k}}\frac{X_l+X_k}{X_l-X_k}=\left(\frac{1+(-1)^{n+1}}{2}\right)1_K, \tag{1}$$
in a family $X=\left(X_k\right)_{1 \leqslant k \leqslant n}$ of $n$ indeterminates, identity taking place in the rational function field $K\left(X\right)=K(X_k)_{1 \leqslant k \leqslant n}$ over a commutative field $K$ (whose unity we denote by $1_K$). A field is an abstract algebraic structure in which one can perform the standard algebraic operations of addition, subtraction, multiplication and division by nonzero elements. A commutative field is a field whose multiplication is commutative (there are indeed examples of noncommutative fields, albeit somewhat rare and particular). I want to invite you -- for the time being -- to take the meaning of this identity involving polynomial indeterminates to be that the corresponding identity is valid for any family $x \in K^n$ of pairwise distinct elements of an arbitrary commutative field (the condition $k \neq l \Rightarrow x_k \neq x_l$ serves of course to ensure the existence of the fractions discussed above, by guaranteeing their denominators are not null). This is ultimately the meaning of "universal polynomial identity": an identity valid for these abstract, universal objects called polynomials entails the validity of the corresponding identity for any family of elements in any commutative ring (hence the"universality").
We would further like to reduce the identity $(1)$ to a purely polynomial form, by taking common denominators, one of which is $\displaystyle\prod_{1 \leqslant k<l \leqslant n}(X_l-X_k)$. Bearing in mind that for each fixed $h$ with $1 \leqslant h \leqslant n$ we have:
$$\begin{align}
\prod_{1 \leqslant k<l \leqslant n}(X_l-X_k)\prod_{\substack{1 \leqslant k \leqslant n\\k \neq h}}\frac{X_k+X_h}{X_k-X_h}&=\prod_{\substack{1 \leqslant k<l\leqslant n\\k, l \neq h}}(X_l-X_k)\prod_{1 \leqslant k<h}(X_h-X_k)\prod_{h<k \leqslant n}(X_k-X_h)\prod_{\substack{1 \leqslant k \leqslant n\\k \neq h}}\frac{X_k+X_h}{X_k-X_h}\\
&=\prod_{\substack{1 \leqslant k<l\leqslant n\\k, l \neq h}}(X_l-X_k)\prod_{1 \leqslant k<h}(-1)\prod_{\substack{1 \leqslant k \leqslant n\\k \neq h}}(X_k+X_h)\\
&=(-1)^{h-1}\prod_{\substack{1 \leqslant k<l\leqslant n\\k, l \neq h}}(X_l-X_k)\prod_{\substack{1 \leqslant k \leqslant n\\k \neq h}}(X_k+X_h),
\end{align}$$
upon multiplying the above identity (1) with this common denonominator we obtain:
$$\sum_{h=1}^n (-1)^{h-1}\prod_{\substack{1 \leqslant k<l\leqslant n\\k, l \neq h}}(X_l-X_k)\prod_{\substack{1 \leqslant k \leqslant n\\k \neq h}}(X_k+X_h)=\left(\frac{1+(-1)^{n+1}}{2}\right)\prod_{1 \leqslant k<l \leqslant n}(X_l-X_k), \tag{2}$$
relation which takes place in the polynomial ring $K[X]=K[X_k]_{1 \leqslant k \leqslant n}$. Since however all the coefficients of this polynomial relation are obviously integers, in order to prove it holds over an arbitrary commutative field $K$ it suffices to establish it in an even more universal setting, namely the integer coefficient polynomial ring $\mathbb{Z}[X]=\mathbb{Z}[X_k]_{1 \leqslant k \leqslant n}$.
Having thus reformulated our task to that of proving a polynomial identity in $\mathbb{Z}[X]$, let us introduce the Vandermonde polynomial $\mathrm{v}\colon=\displaystyle\prod_{1 \leqslant k<l \leqslant n}(X_l-X_k)$ and rewrite the identity (2) in the form:
$$\sum_{h=1}^n\prod_{\substack{1 \leqslant k<l\leqslant n\\k, l \neq h}}(X_l-X_k)\prod_{1 \leqslant k<h}(-X_h-X_k)\prod_{h<k \leqslant n}(X_k-(-X_h))=\left(\frac{1+(-1)^{n+1}}{2}\right)\prod_{1 \leqslant k<l \leqslant n}(X_l-X_k). \tag{3}$$
In order to properly handle this equivalent form, let us recall the
universal property of polynomial rings:
given a family $Y$ of indeterminates indexed by set $I$, a commutative ring $A$ and a family $x \in A^I$ of elements of $A$, there exists a unique ring morphism $\varphi \in \mathrm{Hom}_{\mathbf{Ann}}(\mathbb{Z}[Y], A)$ such that $\varphi(Y_i)=x_i$ for every index $i \in I$. This unique morphism will be referred to as the morphism of substitution with $x$ and for every polynomial $f \in \mathbb{Z}[Y]$ we will denote its substituted image by $f(x)\colon=\varphi(f)$.
Recall also the general Kronecker symbol, given by $\delta_{st}=\begin{cases}0, & s \neq t\\ 1, &s=t \end{cases}$. Introducing for each $h$ with $1 \leqslant h \leqslant n$ the family of polynomials $t_h \in \mathbb{Z}[X]^n$ given by $t_h\colon=\left((-1)^{\delta_{kh}}X_k\right)_{1 \leqslant k \leqslant n}$ – in other words such that $(t_h)_k=\begin{cases}X_k, &k \neq h\\-X_h, &k=h \end{cases}$, we remark that the above form (3) of our identity can also be expressed as:
$$\sum_{h=1}^n \mathrm{v}(t_h)=\frac{1+(-1)^{n+1}}{2}\mathrm{v}. \tag{4}$$
In simpler words, the term of index $h$ in the left-hand sum of identity (3) is obtained by replacing in $\mathrm{v}$ only the indeterminate $X_h$ with its opposite $-X_h$ while keeping the others unchanged, this being the concrete effect of performing the substitution $\mathrm{v}(t_h)$.
The proof of identity (4) will consist in actually expanding all the products which occur as the $n$ terms in the left-hand side sum, and in order to obtain these expansions (essentially, in order to compute the coefficients of the Vandermonde polynomial), we recall the connection between the Vandermonde polynomial and the associated Vandermonde matrix. First we briefly mention a couple of very general phenomena in the context of rings and ring morphisms:
a) consider an arbitrary natural number $r \in \mathbb{N}$, two rings $A$ and $B$ and a ring morphism $f \in \mathrm{Hom}_{\mathbf{Ann}}(A, B)$. The map defined by:
$$\begin{align}
\mathscr{M}_r(f) \colon \mathscr{M}_r(A) &\to \mathscr{M}_r(B)\\
\mathscr{M}_r(f)(M)\colon&=\left(f(M_{kl})\right)_{1 \leqslant k, l \leqslant n}
\end{align}$$
is also a ring morphism, which we shall refer to as the matrix morphism of order $r$ induced by $f$ (recall that by definition a square matrix of order $M$ over $A$ is nothing else than a family of elements of $A$ indexed by the cartesian “square” $[1, r] \times [1, r]$, $[p, q]$ denoting here the natural interval of all natural numbers between $p$ and $q$; the notation $M_{kl}$ therefore refers to the component of index $(k, l)$ of matrix $M$). If $A$ is commutative, $x \in A^I$ is an arbitrary family of elements and $\varphi \colon \mathbb{Z}[Y] \to A$ is the morphism of substitution with $x$, for any matrix $M \in \mathscr{M}_r(\mathbb{Z}[Y])$ we adopt the notation $M(x)\colon=\mathscr{M}_r(\varphi)(M)$.
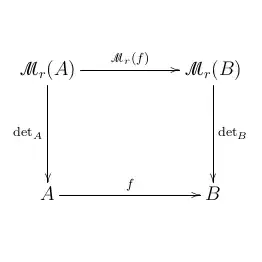
b) in the above setting of a) additionally assume the rings $A$ and $B$ are both commutative, so that we can define the determinant morphisms $\det_A \in \mathrm{Hom}_{\mathbf{Mon}}(\mathscr{M}_r(A), A)$ respectively $\det_B \in \mathrm{Hom}_{\mathbf{Mon}}(\mathscr{M}_r(B), B)$, which are monoid morphisms with respect to the multiplicative monoid structures subjacent to the rings in question (simply put, this means nothing more than the fact that determinants are multiplicative). In this situation the following diagram is commutative, which is a systematic way of saying that $\det_B \circ \mathscr{M}_r(f)=f \circ \det_A$:
and we continue by focusing on the general property of Vandemonde matrices and determinants:
c) let $\mathrm{V} \in \mathscr{M}_n(\mathbb{Z}[X])$ be the universal Vandermonde matrix in the family $X$ of indeterminates, given by $\mathrm{V}_{kl}=X_l^{k-1}$. We have the universal relation $\det \mathrm{V}=\mathrm{v}$ and hence by virtue of proposition b) above the relation $\det \mathrm{V}(x)=\mathrm{v}(x)$ for any family $x \in A^n$ of $n$ elements of an arbitrary commutative ring $A$.
In particular, it follows that $\mathrm{v}(t_h)=\det \mathrm{V}(t_h)$ for any $h$ such that $1 \leqslant h \leqslant n$. For arbitrary $m \in \mathbb{N}$ we write $\Sigma_m$ for the symmetric group of degree $m$, which is the group of all permutations of the natural interval $[1, m]$. We recall that for any commutative ring $A$ and for any square matrix $M \in \mathscr{M}_m(A)$ of order $m$ over $A$ we have the following expression for the determinant of $M$:
$$\det M=\sum_{\sigma \in \Sigma_m} \mathrm{sgn}(\sigma)\prod_{k=1}^m M_{k\sigma(k)}=\sum_{\sigma \in \Sigma_m}\mathrm{sgn} (\sigma) \prod_{k=1}^m M_{\sigma(k)k}.$$
Since by definition we have $\mathrm{V}(x)_{kl}=x_l^{k-1}$ for any family $x \in A^n$ of elements in a commutative ring $A$, it follows in particular that $\mathrm{V}(t_h)_{kl}=\left((-1)^{\delta_{hl}}X_l\right)^{k-1}$ and therefore that:
$$\begin{align}\mathrm{v}(t_h)&=\det \mathrm{V}(t_h)\\
&=\sum_{\sigma \in \Sigma_n} \mathrm{sgn}(\sigma)\prod_{k=1}^n \left((-1)^{\delta_{kh}}X_k\right)^{\sigma(k)-1}\\
&=\sum_{\sigma \in \Sigma_n} \mathrm{sgn}(\sigma)(-1)^{\sigma(h)-1}\prod_{k=1}^n X_k^{\sigma(k)-1},
\end{align}$$
where we also keep in mind that:
$$\mathrm{v}=\det \mathrm{V}=\sum_{\sigma \in \Sigma_n} \mathrm{sgn}(\sigma)\prod_{k=1}^n X_k^{\sigma(k)-1}.$$
Having obtained these explicit expressions, we substitute them in the left-hand term of (4) in order to deduce that:
$$\begin{align}
\sum_{h=1}^n \mathrm{v}(t_h)&=\sum_{h=1}^n \sum_{\sigma \in \Sigma_n} \mathrm{sgn}(\sigma)(-1)^{\sigma(h)-1}\prod_{k=1}^n X_k^{\sigma(k)-1}\\
&=\sum_{\sigma \in \Sigma_n} \sum_{h=1}^n \mathrm{sgn}(\sigma)(-1)^{\sigma(h)-1}\prod_{k=1}^n X_k^{\sigma(k)-1}\\
&=\sum_{\sigma \in \Sigma_n} \left(\sum_{h=1}^n (-1)^{\sigma(h)-1}\right) \mathrm{sgn}(\sigma)\prod_{k=1}^n X_k^{\sigma(k)-1}\\
&=\sum_{\sigma \in \Sigma_n} \left(\sum_{h=1}^n (-1)^{h-1}\right) \mathrm{sgn}(\sigma)\prod_{k=1}^n X_k^{\sigma(k)-1}\\
&=\left(\sum_{h=0}^{n-1} (-1)^h\right) \mathrm{v}\\
&=\frac{(-1)^n-1}{-1-1}\mathrm{v}\\
&=\frac{1+(-1)^{n+1}}{2}\mathrm{v},
\end{align}$$
which shows that our identity is indeed valid.
This expound is somewhat pedantic and detailed, however you should not be too daunted by its appearance, for the statements made within are ultimately quite simple and intuitively clear (as we are almost exclusively handling substitutions in a variety of algebraic expressions). The more abstract formulations of results valid in general algebraic settings I deemed fit to include here so as to serve you in your process of deepening your mathematical knowledge and capacity for abstraction.
