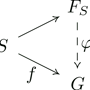The word "free" in mathematics had a categorical meaning. Whenever you see the term "a free X" then you should be thinking "a free object in the category X".
Free groups. Your previous question gives the definition of a free group as the free object in the category of groups:
Let $S$ be a set. A free group on $S$ is a group such that for any group $G$ and any map $f:S\to G$, there exists a unique homomorphism $\varphi:F(S)\to G$ extending $f$.
That is, there exists a unique homomorphism $\varphi$ such that the following diagram (image from wikipedia) commutes:
Then existence and uniqueness can be proven, so we can talk about the free group on $S$, and in fact it turns out that it is the cardinality of the set which matters, rather than the set itself (this is kinda obvious if you are used to thinking of groups as being "up to isomorphism"). As there are two-generated groups which are non-abelian, it is an easy exercise to use the above definition to prove that if $|S|>1$ then $F(S)$ is non-abelian. Slightly trickier is to prove that if $|S|=1$ then $F(S)\cong\mathbb{Z}$, but this yields the following:
A free group $F(S)$ is abelian if and only if $|S|=1$.
Free abelian groups. Okay, so that is the categorical view of a free group. Lets now switch categories to the category of abelian groups:
Let $S$ be a set. A free abelian group on $S$ is a group such that for any abelian group $G$ and any map $f:S\to G$, there exists a unique homomorphism $\varphi:FA(S)\to G$ extending $f$.
I made the word "abelian" bold as the two definitions are identical, except for this word (which has changed the category). The wikipedia article on free abelian groups does not have a diagram I can borrow, but if it did it would be identical to the free group one, apart from the label "$F_S$" which would be replaced with the label "$FA(S)$". It turns out that there is a nice description of free abelian groups on finite sets: if $S$ is a finite set then $FA(S)\cong \mathbb{Z}^{|S|}$.
We can similarly define the free nilpotent group on $S$ of class $n$, the free soluble group on $S$ of class $n$, free semigroups, free monoids, free abelian monoids, free lattices, and so on.
Free products. Free objects have a completely categorical definition (they are the "free object in the category X"). Free products of groups don't quite fit into the "free object" framework, but they sort of do (they are kind of the "free object in the category of products of groups", but I have no idea if the "category of products of groups" makes sense!). Anyway, the free product can be defined completely categorically, as it is the coproduct in the category of groups:
The free product of the groups $G$ and $H$ is a group $G\ast H$ with homomorphisms $\iota_G:G\rightarrow G\ast H$ and $\iota_H:H\rightarrow G\ast H$ such that given any other group $X$ with homomorphisms $f_G:G\rightarrow X$ and $f_H:H\rightarrow X$ there is a unique homomorphism $f:G\ast H\rightarrow X$ where $f_G=f\circ\iota_G$ and $f_H=f\circ\iota_H$.
It just so happens that the explicit constructions free groups and of free products are similar, and it is these definitions most people use on a day-to-day basis. However, it is always helpful to keep these categorical considerations in mind, especially as they link to other notions and ideas.
Coproducts, like free objects, are defined completely categorically, so we can ask if the category of abelian groups has a coproduct. It does: it is simply the direct product (the finitely-based Cartesian product).