2

Let $x_i$ be the coordinates of a two-dimensional vector and let $x^\prime_i$ be the coordinates of the vector rotated by an angle $\theta$ in the plane. The components of the two vectors are related by a transformation as $$x^\prime_j = R_{ij} x_i$$ where $R_{ij}$ is a rotation matrix. This is a representation of the rotation group.

Specifically, a rotation by an angle $\theta$ in two dimensions matrix, $$ R(\theta) = \begin{pmatrix} \cos\theta & \sin \theta\\ - \sin \theta & \cos\theta \\ \end{pmatrix} $$

we do we got this matrix, can someone show me the argument or visualization?

mathphy
  • 853
  • Hint: Represent two dimensional vectors as the Euler representation of complex numbers ($R\cos(\theta_1) + Ri\sin(\theta_1)$), and use DeMoivre's Theorem. Here, $R = ||x_j||$ and $\theta_1 = \arg{(x_j)}$. – ThisIsNotAnId May 03 '13 at 20:34
  • Duplicate of Understanding rotation matrices. Information is also in solutions to http://math.stackexchange.com/questions/352004/geometrical-proof-of-a-rotation/352013#352013 http://math.stackexchange.com/questions/286039/where-did-this-matrix-come-from/286051#286051, – rschwieb May 03 '13 at 20:35

2 Answers2

3

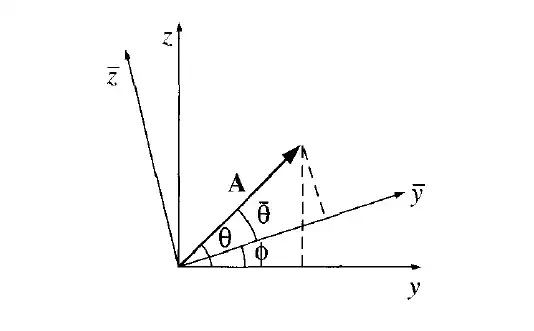According to the picture, for the first coordinates: enter image description here $$A_y=Acos(\theta)$$ $$A_z=Asin(\theta)$$

now write $\mathbf A$ in terms of new coordinates:

$$\bar{A_y}=Acos(\bar{\theta})=Acos(\theta - \phi)=A(cos\theta cos\phi +sin\theta sin\phi)=A_ycos\phi+A_zsin\phi$$

$$\bar{A_z}=Asin \bar{\theta}=Asin(\theta-\phi)=A(sin\theta cos\phi-cos\theta sin\phi)=-sin\phi A_y+A_zcos\phi$$ and writing this relations in matrix form, we will get the given formula.

$$ \begin{pmatrix} \cos\phi & \sin \phi\\ - \sin \phi & \cos\phi \\ \end{pmatrix} $$

Mostafa
  • 521
1

I suggest drawing a diagram and working it through.

To simplify matters, you could consider the unit vectors on the $x$ and $y$ axes and what the rotation does to them, to see that the matrix must be as it is (draw diagrams - they are very easy - and work out the components of the transformed unit vectors).

Then think about why, if you rotate the $x$ and $y$ components of a vector by $\theta$, you rotate the vector itself through $\theta$ (if the orientations are all the same).

[Another way of looking at it - rotating a vector clockwise is the same as rotating the axes anticlockwise by the same amount]

I recommend working at it, because when it clicks it can become one of those beautiful things where different insights play off each other (de Moivre's theorem, for example).

Mark Bennet
  • 101,769