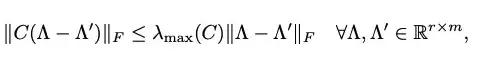I am trying to proof the following inequality (source, equation 17):
where $C \in R^{n\times n}$. I tried the following:
$$||C (\Lambda - \Lambda^T)||_F \le ||C||_F ||\Lambda - \Lambda^T || = \sqrt{\sum \lambda_i(C)} || \Lambda - \Lambda^T||_F$$
But I don't understand how to pursue farther. How to prove that the square root of the eigenvalues summation is less than the max eigenvalue?