A problem concerning a parallelogram and a circle

Question

Sorry for the ambiguous title. If you can phrase it better, feel free to edit.

"A parallelogram $ABCD$ has sides $AB = 16$ and $AD = 20$. A circle, which passes through the point $C$, touches the sides $AB$ and $AD$, and passes through sides $BC$ and $CD$ at points $M$ and $N$, such that $\frac{BM}{MC} = \frac{1}{8}$. Find $\frac{DN}{NC}$."

Apparently, I'm supposed to solve this using triangle similarity, because that's the chapter's name (But I'm open to other answers too!). I've tried marking the center of the circle and going from there, creating triangles and seeking similarity. But couldn't really go far without it getting overly complicated.

Here's the picture:

Answer 1

Let $ x =AL = AK$ then $DL = 20-x$ and $BK = 16-x$. Also $BM = 20/9$

By the PoP with respect to $B$ we have $$BM\cdot BC = BK^2\implies BK = 20/3\implies x= 28/3$$

By the PoP with respect to $D$ we have $$DN\cdot DA = DL^2\implies DL = ...$$

Answer 2

We have to be careful because the given picture is misleading, actually $K$ and $L$ lie outside $ABCD$.

We have $BM\cdot BC = \frac{1}{9}BC^2 = \frac{400}{9}=BK^2$, hence $BK=\frac{20}{3}$ and $AL=AK=16+\frac{20}{3}=\frac{68}{3}$, such that $DL=\frac{8}{3}$. This gives $DN\cdot DC=\frac{64}{9}$, hence $DN=\frac{4}{9}$ and $\frac{DN}{NC}=\frac{4/9}{16-4/9}=\color{red}{\frac{1}{35}}$.

There is a second solution with $\widehat{DAB}\approx 96.38^\circ$ and $\frac{DN}{NC}=\color{red}{\frac{4}{5}}$; in this case $K$ and $L$ properly lie on $AB$ and $AD$. This is probably the intended solution if we label the vertices of $ABCD$ counter-clockwise, as usually done.

Answer 3

Different from power of a point solution:
Vectors.
Let $b:=\overrightarrow{AB}$, $\;d:=\overrightarrow{AD}$, $c:=\cos\angle BAD$.
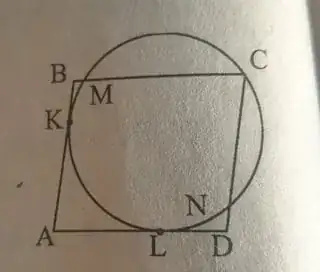
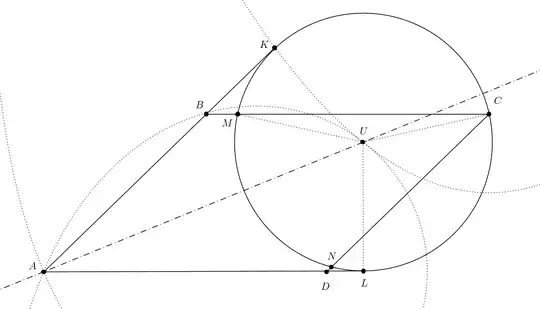
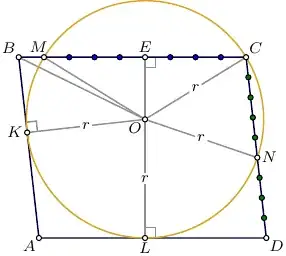
It's given that $|\overrightarrow{AB}|=16$, $\;|\overrightarrow{AD}|=20$, $\;\overrightarrow{AM}=b+\frac19 d$ and $\rho(O,AB)$ $=\rho(O,AD)$ $=OC$ $=OM$.
$\rho(O,AB)=\rho(O,AD)$ implies $AO$ is the bisector of $\angle BAD$ thus $\overrightarrow{AO}||\left( \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}+ \frac{\overrightarrow{AD}}{|\overrightarrow{AD}|} \right)$.

Let $\overrightarrow{AO}=t(5b+4d)$ for some $t$. We find $\rho(O,AD)=\sqrt{(\overrightarrow{AO})^2-\left(b \dfrac{\overrightarrow{AO}\cdot b}{|b|^2}\right)^2}$

Then we have $$ \begin{cases} (t(5b+4d)-(b+d))^2=(t(5b+4d)-(b+\frac19 d))^2\\ (t(5b+4d)-(b+d))^2=(t(5b+4d))^2-\frac{1}{b^2}\left(t(5b+4d)\cdot b\right)^2 \end{cases} $$ Having $b^2=16^2$, $\;d^2=20^2$, $\;bd=16\cdot 20\cdot c$ we feed this thing to wolframalpha(1, 2, 3), obtaining $$ \begin{cases} (180 c + 180) t = 36 c + 25\\ (10 c^2 + 10) t^2 + c (20 t^2 - 9 t + 1) - 9 t = -\frac{41}{40} \end{cases} $$ $$ \left[ \begin{array}{l} \begin{cases} c = -\frac{1}{9}\\ t = \frac{21}{160} \end{cases}\\ \begin{cases} c = \frac{13}{18}\\ t = \frac{51}{310} \end{cases} \end{array} \right. $$ Now let $\overrightarrow{AN}=ub+d$, with $(\overrightarrow{OC})^2=(\overrightarrow{ON})^2$ $$(t(5b+4d)-(b+d))^2=(t(5b+4d)-(ub+d))^2$$ which gives (4, 5, 6) $u=\frac{4}{9}$ in the first case ($\frac{DN}{NC}=\frac{u}{1-u}=\frac{4}{5}$) and $u=\frac{1}{36}$ ($\frac{DN}{NC}=\frac{u}{1-u}=\frac{1}{35}$) in the second case almost for free, alone to say the computations are almost unbearable by hand)

Answer 4

As @Jack D'Aurizio noted, the OP picture is misleading, but if we assume that $\angle BAD$ is obtuse, it make more sense:

Let $|AB|=|CD|=a$, $|BM|=u$, $|MC|=8u$ then $|AD|=|BC|=4u$, $|ME|=|EC|=4u$, and we can find

\begin{align} |BK|^2&=u\cdot9u ,\\ |BK|&=3u ,\\ |AK|=|AL| &=a-3u ,\\ |DL|&=12u-a ,\\ |DN|\cdot|CD|&=|DL|^2 ,\\ |DN|&=\frac{|DL|^2}{|CD|} =\frac{(12u-a)^2}a ,\\ |CN|&=a-\frac{(12u-a)^2}a \\ \frac{|DN|}{|CN|} &= \frac{(12u-a)^2}{24u(a-6u)} . \end{align}

And for $a=16$, $u=\tfrac{20}9$,

\begin{align} \frac{|DN|}{|CN|}&=\tfrac45 . \end{align}