The question is as follows: You are given a 100-sided die. After you roll once, you can choose to either get paid the dollar amount of that roll OR pay one dollar for one more roll. What is the expected value of the game? There is no limit on number of rolls.
The EV for a 100-sided die roll is 50.5, but the fact that you can pay a dollar for an extra roll complicates things. Not quite sure how to proceed.
If the expected value of this game is $a$, then at a die roll of $X$ you have the choice of either collecting $X$ or paying a dollar and restart, which gives you an expected value of $a-1$. To maximize the expected value, you should take $X$ if $X> a-1$ and start over if $X\le a-1$ (it does not really matter what we do when $X=a-1$). We obtain therefore $$ a = \frac1{100}\left(\lfloor a-1\rfloor\cdot a+\sum_{k=\lfloor a-1\rfloor+1}^{100}k\right) =\frac1{100}\left(\lfloor a-1\rfloor\cdot a+\frac{100\cdot101}{2}-\frac{\lfloor a-1\rfloor \cdot\lfloor a\rfloor}{2}\right). $$ I find numerically (didn't do much code checking, but the results are somewhat plausible) $$a\approx87.3571 $$ which seems to be exactly (and of course the true result must be rational) $$a=87\frac{5}{14}.$$ But I'm sure you can do the justification after the fact, i.e. show that the strategy that consists in continuing until you roll at least $87$ gives you $87\frac{5}{14}$ as expected value.
For your convenience, here is the PARI one-liner:
solve(a=1,100,sum(k=1,100,max(a-1,k))/100-a)
If an extra roll costs two dollars instead of one, the result would be $$a=82\frac12$$ instead, and with a cost of only $0.1$ dollars it would be $$a=96\frac1{10}.$$
Hint:
If your value now is $X_t$, what is the marginal value of the roll? If you roll $R \sim \mathcal{U}[1,100]$, then if $R > X_t+1$ you gained and if $R \leq X_t+1$, you either lost or became indifferent. So what is the marginal value?
A different approach, more complicated, is this:
Suppose that we can play a game as many times as we wish, and $\{J_n\}_{n\in\mathbb{N}}$ is an i.i.d. sequence where each $J_k$ is the possible gain in the $k$-th game. Now suppose that every time we play we pay a fixed amount $c$ and that we can stop playing at any time, giving the total gain $G_k:=J_k-ck$ if we stop at time $k$.
Further suppose that we set a threshold $T$ such that we stop playing when $J_k\geqslant T$ for the first time, otherwise we play again.
Then the expected gain using the threshold strategy, for given $T$, will be $\operatorname{E}[G_S]$ where $S$ is the time where the game stops. Then we have that $$ \operatorname{E}[G_S]=\sum_{k\geqslant 1}\operatorname{E}[G_S|S=k]\Pr [S=k]=\sum_{k\geqslant 1}\operatorname{E}[G_k|S=k]\Pr [S=k] $$ because playing countable number of games we assume a discrete time $k$. Now observe that $$ \operatorname{E}[G_k|S=k]=\operatorname{E}[J_1|J_1\geqslant T]-ck,\quad \Pr[S=k]=q^{k-1}p\\\text{ for }\quad q:=1-p,\quad p:=\Pr [J_1\geqslant T] $$
Therefore
$$ \begin{align*} \operatorname{E}[G_S]&=\sum_{k\geqslant 1}\operatorname{E}[G_S|S=k]\Pr [S=k]\\ &=p\sum_{k\geqslant 1}(\operatorname{E}[J_1|J_1\geqslant T]-ck)q^{k-1}\\ &=p\left(\frac{\operatorname{E}[J_1|J_1\geqslant T]}{1-q}-\frac{c}{(1-q)^2}\right)\\ &=\operatorname{E}[J_1|J_1\geqslant T]-\frac{c}{p}\\ &=\frac{\operatorname{E}[J_1 \mathbf{1}_{\{J_1\geqslant T\}}]-c}{\Pr [J_1\geqslant T]} \end{align*} $$
What will be the optimal value for $T$ if $J_1\sim \operatorname{Unif}(\{1,\ldots ,n\})$? In this case we want to maximize $$ \operatorname{E}[G_S]=\frac1{2}\cdot \frac{(n+1-2c)n-T^2+T}{n+1-T},\quad T\in\{1,\ldots ,n\} $$ For $c=1$ and $n=100$ we get that $T=87$ maximizes the expected gain, giving $\operatorname{E}[G_S]\approx 86.3$.
Same puzzle at Expected value of game involving 100-sided die and Let's play a dice game
If the dice shows at least $x+1$ we take take that results else for the dice game; when dice shows x or less we re-throw dice and take a penalty $(x-c)$ where $c=1$ which occurs with probability $x/100,$ so our expectation x is
$$E[X] = E[X|X > x] + x/100 \cdot (E[X] - c)$$ $$x = 1/100 \cdot \sum^{100}_{k=x+1} k + x/100 \cdot (x-c)$$ $$100 \cdot x = \left[\sum^{100}_{k=1} k - \sum^{x}_{k=1} k \right] + x \cdot (x-c)$$ $$100 \cdot x = \left[100 \cdot 101/2 - x \cdot (x+1)/2 \right] + x \cdot (x - c)$$ $$200 \cdot x = 100 \cdot 101 - x \cdot (x+1) + 2 \cdot x \cdot (x - c)$$ $$200 \cdot x = 10100 - x^2-x + 2 \cdot x^2 - 2 \cdot c \cdot x$$ $$0 = x^2 - (201 + 2c) \cdot x + 10100$$
quadratic formula for c=1
$$x_{1/2} = (203 \pm \sqrt(203^2 - 4 \cdot 10100)/2$$ $$x_1 = 0.5 \cdot (203 - \sqrt(809) = 87.27854$$ (ignore $$x_2 = 0.5 \cdot (203 + \sqrt(809)=115.7 > 100)$$
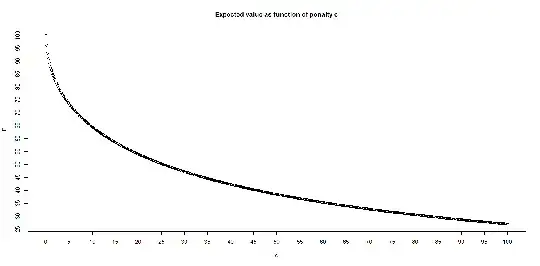
a few special cases for different penalties of c to throw 100-sided dice again, computed in R:
$$f <- function(x,c) {x^2 - (201+2*c)*x + 10100}$$
$$uniroot(f,c(1,100),tol=0.0001,c=0.1) => 96.08781$$ $$uniroot(f,c(1,100),tol=0.0001,c=0.5) => 90.95011$$ $$uniroot(f,c(1,100),tol=0.0001,c=1) => 87.27854$$ $$uniroot(f,c(1,100),tol=0.0001,c=2) => 82.34436$$ $$uniroot(f,c(1,100),tol=0.0001,c=3) => 78.75632$$ $$uniroot(f,c(1,100),tol=0.0001,c=5) => 73.40249$$ $$uniroot(f,c(1,100),tol=0.0001,c=10) => 64.56254$$
