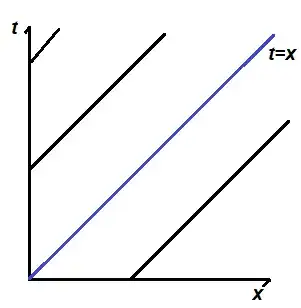
The well-known age-structure/transport equation by McKendrick and von Foerster has the form: $$\frac{\partial }{\partial t} u(t,x) + \frac{\partial }{\partial x} u(t,x) = -\lambda u(t,x), \quad \quad \text{for }t>0 \text{ and } 0<x<\tau,$$ which is subjected to the boundary and initial conditions: $$u(t,0) = cq(t), \quad u(0,x) = f(x)$$ Here, $q(t), f(x)$ are known smooth functions. Using the method of characteristic, I get $$\frac{dt}{ds} = 1, \quad \frac{dx}{ds} = 1, \quad \frac{dz}{ds} = -\lambda z,$$ with initial conditions $t(r,0) = r, x(r,0) = 0,$ and $z(r,0) = cq(r)$. Solving the ode's, I obtain $$x(r,s) = s, \quad t(r,s) = s+r, \quad z(r,s) = cq(r)e^{-\lambda s}.$$ Thus, $s = x$ and $r = t - x$. Together, I obtain: $$u(t,x) = z(t-x,x) = cq(t-x)e^{-\lambda x}.$$
Looking at the "trivial" solution, I find that this is only half of the solution, which corresponds to $t>x$. The other half is important because it helps to prescribe the "history" of the solution (e.g. transform into delay equation). Please point me to how I can find the other half when $0<t\leq x$. Thank you!