1

I am attempting to find a generalised formula for the normal of a simplex facet in n-dimensions.

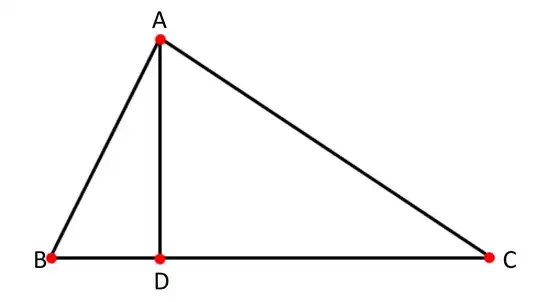
For example if I had the 2 dimensional simplex formed by the vertices ABC below. Then I want to find the normal for the facet formed by the vertices BC. The reason I want the normal is because I'm trying to find the hyperplane that intersects vertices BC, and is equal to 1 at vertex A. Is there a nice way of doing this?

One way I thought of would be to find D. and then use the formulas: $$W = \frac{A-D}{||A-D||_2}$$ $$b = -D\cdot{W}$$ for the plane: $$xW + b = y$$ However, I don't know how to find D for an n-dimensional simplex facet either.

I'm not very knowledgeable in linear algebra or geometry, so any help would be great.

Example

Community
  • 1
Michael Murray
  • 133
  • 1
  • 9

1 Answers1

3

Let $x_0,\ldots,x_n$ be the vertices of the $n$-dimensional simplex.

You can find all normals of the facets using the inverse of the following matrix: $$ \begin{pmatrix} \;\; & x_0^T & \;\; & 1 \\ \;\; & x_1^T & \;\; & 1 \\ \;\; & \vdots & \;\; & \vdots \\ \;\; & x_n^T & \;\; & 1 \\ \end{pmatrix} $$ Note that this matrix is invertible unless the simplex is degenerate. The determinant of this matrix is $\pm n!$ times the volume of the simplex.

Let's compose the inverse of the matrix of vectors $y_0,\ldots,y_n \in\mathbb{R}^n$ and numbers $c_0,\ldots,c_n\in\mathbb{R}$ as follows: $$ \begin{pmatrix} \;\; & x_0^T & \;\; & 1 \\ \;\; & x_1^T & \;\; & 1 \\ \;\; & \vdots & \;\; & \vdots \\ \;\; & x_n^T & \;\; & 1 \\ \end{pmatrix} \begin{pmatrix} \; & & & \; \\ y_0 & y_1 & \cdots & y_n \\ \; & & & \; \\ -c_0 & -c_1 & \cdots & -c_n \end{pmatrix} = \begin{pmatrix} 1 & & & 0 \\ & 1 & & \\ & & \ddots & \\ 0 & & & 1 \end{pmatrix} $$ Then you get $\langle x_i\, ,\,y_i\rangle = 1+c_i$ and $\langle x_i\, ,\,y_k\rangle = c_k,\;i\neq k.$ This means $$ i\neq k,\,j\neq k\; \Rightarrow \; \langle x_i-x_j\, , \,y_k \rangle =\langle x_i\, , \,y_k \rangle - \langle x_j\, , \,y_k \rangle = c_k - c_k = 0 $$ which shows that $y_k$ is perpendicular to the facet opposite to $x_k.$

Note that the vectors $y_k$ are not necessarily unit vectors. You might have to scale them.

Reinhard Meier
  • 8,302
  • That is just what I was looking for, thank you so much! – Michael Murray May 21 '20 at 11:25
  • You are welcome! – Reinhard Meier May 21 '20 at 11:28
  • Isn't some generalized cross product a better approach? Or perhaps that ends up being some optimal plan for computing the matrix inverse I suppose? – safetyduck Feb 26 '22 at 09:09
  • @mathtick Maybe there is a way of solving this by means of a generalized cross product. But how do you use generalized cross products to get all the normals of the simplex in one go? I assume that this would boil down to matrix inversion anyway, if you tried to do it efficiently. – Reinhard Meier Feb 27 '22 at 11:04
  • @ReinhardMeier this is pretty good https://math.stackexchange.com/questions/1587319/surface-area-of-k-simplex-in-mathbbrk/2098632#2098632 I have not quite finished implementing yet but I think it might be ok – safetyduck Feb 28 '22 at 14:11