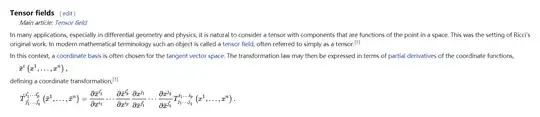
The Kronecker delta is
and I use the definition of tensor as
I try to prove the Kronecker delta is a (1,1) tensor. I find the following equation which is enough to show Kronecker delta is a tensor. $$ {\delta'}_j^i = \delta_k^k \frac{\partial{x_i}'}{\partial{x_k}}\frac{\partial{x_k}}{\partial{x_j}'} $$ But I dnot know how to get the equation.