The strategy for deriving the envelope of a family of curves is typically done in Cartesian coordinates, so I'll use them. For completeness, I'll derive OP's line equation. To avoid fractions, I'll use an angle $\phi$ that is half OP's angle $\alpha$.
In the unit circle, the light ray from $P=(-1,0)$ to $Q=(\cos2\phi,\sin2\phi)$ reflects to the point $P'$ diametrically opposite the point $P''=(\cos4\phi,\sin4\phi)$. Therefore, $P'=-P''$. The line $QP'$ is then
$$x \sin3\phi - y \cos 3\phi - \sin\phi = 0 \tag{1}$$
(which, upon substituting $(x,y)\to(r\cos\theta, r\sin\theta)$ and simplifying, agrees with OP's polar version). To get at the envelope of the lines, we differentiate $(1)$ with respect to the parameter $\phi$:
$$3x\cos3\phi+3y\sin3\phi-\cos\phi = 0 \tag{2}$$
and then we attempt to eliminate $\phi$ from $(1)$ and $(2)$. This gets somewhat tricky. See the edit history for an approach the ventures through the complex realm; I'm replacing that with something slightly more straightforward.
Anticipating a needed translation to put the cusp of the cardioid at the origin, let's substitute $x\to x+1/3$. This, along with the identities
$$\sin 3\phi = \sin\phi (3 - 4\sin^2\phi) \qquad \cos3\phi = \cos\phi (1 -4\sin^2\phi) \tag{3}$$ gives
$$\begin{align}
x \sin3\phi - y \cos3\phi &= 4a\sin^3\phi \tag{1'} \\[4pt]
x \cos3\phi + y \sin3\phi &= 4a\sin^2\phi \cos\phi \tag{2'}
\end{align}$$
where $a:=1/3$. Let us also return to polar coordinates:
$$\begin{align}
r \cos\theta \sin3\phi - r \sin\theta \cos3\phi &= 4a\sin^3\phi \tag{1''} \\[4pt]
r \cos\theta \cos3\phi + r \sin\theta \sin3\phi &= 4a\sin^2\phi \cos\phi \tag{2''}
\end{align}$$
Squaring and adding, we find
$$r^2 = 16a^2 \sin^4\phi \quad\to\quad \sin^2\phi = \frac{r}{4a} \tag{4}$$
Now, substituting from $(3)$ into $(1')$, isolating $\cos\phi$, and squaring, we obtain an equation we can write with even powers of $\sin\phi$ alone. Substituting from $(4)$ yields
$$(r-2 a(1-\cos\theta) ) ((r - 2 a)^2 - 2 a^2 (1 -\cos\theta)) = 0 \tag{1'''}$$
Taking the second factor as extraneous, our envelope has polar equation
$$r = 2 a(1-\cos\theta)\tag{$\star$}$$
which is, in fact, that of a cardioid.
Incidentally, the second factor of $(1''')$ can be written as
$$(r-2a)^2-4a^2\sin^2\frac{\theta}{2} = \left(r-2a\left(1-\sin\frac{\theta}{2}\right)\right)\left(r-2a\left(1+\sin\frac{\theta}{2}\right)\right)$$
so that the trio of curves represented by $(1''')$ looks like
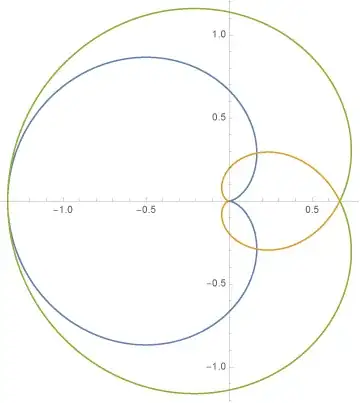
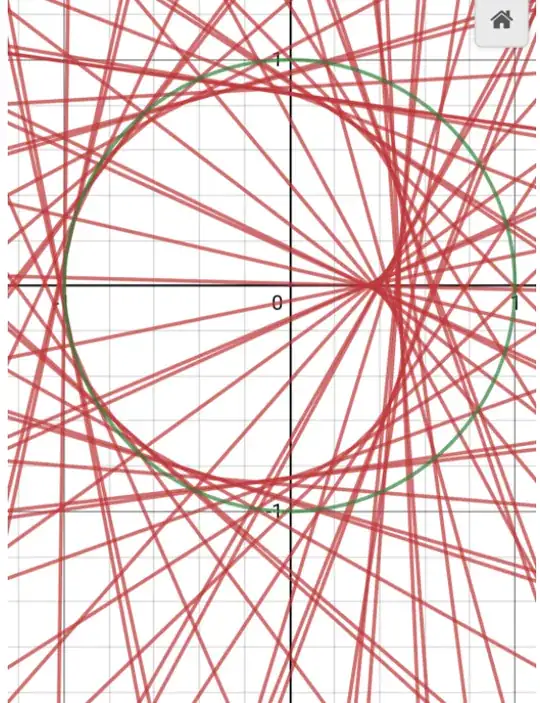Link to image: https://ibb.co/ngJD4jc
