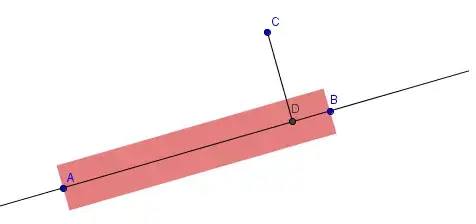
Let the line segment endpoints be $\vec{p}_0 = (x_0 , y_0)$ (A in OP's diagram) and $\vec{p}_1 = (x_1 , y_1)$ (B in OP's diagram), and the point to be tested $\vec{p} = (x, y)$ (C in OP's diagram).
First, calculate
$$t = \frac{(\vec{p} - \vec{p}_0)\cdot(\vec{p}_1 - \vec{p}_0)}{(\vec{p}_1 - \vec{p}_0)\cdot(\vec{p}_1 - \vec{p}_0)} = \frac{ (x - x_0)(x_1 - x_0) + (y - y_0)(y_1 - y_0) }{ (x_1 - x_0)^2 + (y_1 - y_0)^2 } \tag{1}\label{AC1}$$
If $0 \le t \le 1$, the point on the line (D in OP's diagram) closest to the point to be tested (C in OP's diagram) is between the line segment endpoints.
Then, calculate the distance squared between the point to be tested $\vec{p}$, and the point on the line segment closest to that point:
$$d^2 = \left\lVert \vec{p} - \bigr( (1 - t)\vec{p}_0 + t \vec{p}_1 \bigr)\right\rVert^2 = \bigr( x - x_0 - t ( x_1 - x_0) \bigr )^2 + \bigr( y - y_0 - t ( y_1 - y_0 ) \bigr )^2 \tag{2}\label{AC2}$$
If the total line thickness is $w$, the point to be tested $\vec{p}$ is on the line if
$$d^2 \le \left(\frac{w}{2}\right)^2 = \frac{1}{4} w^2$$
In other words, if and only if
$$\left\lbrace ~ \begin{aligned}
0 \le & t \le 1 \\
~ & d^2 \le \frac{1}{4} w^2 \\
\end{aligned} \right . \tag{3}\label{AC3}$$
is the point $\vec{p}$ (point C in OP's diagram) within the "line segment" between $\vec{p}_0$ and $\vec{p}_1$, thickness $w$, and butt caps.
How did we do the above, and why?
First, we parametrise the location of the point D in OP's diagram, $\vec{p}_d = (x_d , y_d)$, as linear interpolation between $\vec{p}_0$ and $\vec{p}_1$:
$$\vec{p}_d(t) = (1 - t) \vec{p}_0 + t \vec{p}_1 = \vec{p}_0 + t (\vec{p}_1 - \vec{p}_0) \tag{A}\label{A}$$
Here, $\vec{p}_d$ is a vector-valued function of parameter $t$, with $\vec{p}_d(0) = \vec{p}_0$ and $\vec{p}_d(1) = \vec{p}_1$. If $0 \le t \le 1$, $\vec{p}_d(t)$ is within the line segment endpoints, otherwise it is elsewhere on the extended line.
Point $\vec{p}_d(t)$ is closest to $\vec{p}$ when their distance is minimized, or when the vector between them is perpendicular to the vector between the line segments. The former occurs when the derivative of the distance or distance squared is zero; the latter is much easier. That is, the line between $\vec{p}_d(t)$ and $\vec{p}$ is perpendicular to the line between $\vec{p}_0$ and $\vec{p}_1$ if and only if
$$\left(\vec{p}_d(t) - \vec{p}\right) \cdot \left(\vec{p}_0 - \vec{p}_1\right) = 0 \tag{B1}\label{B1}$$
which in Cartesian coordinate form is equivalent to
$$(x_0 + t (x_1 - x_0) - x)(x_1 - x_0) + (y_0 + t (y_1 - y_0) - y)(y_1 - y_0) = 0 \tag{B2}\label{B2}$$
To solve this for $t$, we simplify and rearrange it to
$$t \bigr( (x_1 - x_0)(x_1 - x_0) + (y_1 - y_0)(y_1 - y_0)\bigr) - (x - x_0)(x_1 - x_0) - (y - y_0)(y_1 - y_0) = 0$$
and finally to
$$t = \frac{ (x - x_0)(x_1 - x_0) + (y - y_0)(y_1 - y_0) }{ (x_1 - x_0)^2 + (y_1 - y_0)^2 } \tag{C}\label{C}$$
This is equivalent to the first equation in this answer, $\eqref{AC1}$, and tells us where the point on the line closest to $\vec{p}$ is.
It is between the line endpoints if and only if $0 \le t \le 1$.
Next, we need to find the distance between the point at hand, $\vec{p}$, and this closest point on the line $\vec{p}_d(t)$. Euclidean distance, i.e. $\left\lVert \vec{v} \right\rVert = \sqrt{\vec{v} \cdot \vec{v}}$, does perfectly.
However, because square root is a monotonically increasing function of its argument, we can compare squared distances instead of distances. Mathematically, given $0 \le L \in \mathbb{R}$ and $0 \le S \in \mathbb{R}$ (both $L$ and $S$ are nonnegative real numbers),
$$\begin{array}{cc}
L \lt S & \iff & L^2 \lt S^2 \\
L \le S & \iff & L^2 \le S^2 \\
L = S & \iff & L^2 = S^2 \\
L \ge S & \iff & L^2 \ge S^2 \\
L \gt S & \iff & L^2 \gt S^2 \\
\end{array}$$
This means that we can always compare squared distances instead of comparing distances. Thus, we don't need to do the annoying square root operation, which is nice.
The Euclidean distance squared $d^2$ between $\vec{p}$ and $\vec{p}_d(t)$ is
$$d^2 = \bigr(\vec{p} - \vec{p}_d(t)\bigr)\cdot\bigr(\vec{p} - \vec{p}_d(t)\bigr)$$
which written in Cartesian coordinate form, using $\vec{p}_d(t) = \vec{p}_0 + t (\vec{p}_1 - \vec{p}_0) = (1 - t) \vec{p}_0 + t \vec{p}_1$, gives us the equation $\eqref{AC2}$ near the beginning of this answer.