0

The definition of right continuous process:

A stochastic process $(t,\omega) \mapsto X(t,\omega) = X_t(\omega)$ is called right-continuous (left-continuous) if, and only if, $$t \mapsto X_t(\omega)$$ is right-continuous (left-continuous) for all $\omega \in \Omega$.

Starting with an example to define a random variable in continuous time. A random variable is X is a function from the sample space $\Omega$ to the set of real numbers: $$X: \Omega \mapsto R $$ Which also needs to be measurable in measure-theory.

Let's say we have a fair coin. If we throw it once we have:

$\Omega$ = {$\omega_1$} = {H,T} or $\Omega$ = {H,T}

Now let's define our probability function P. The probability of getting a H or T is $\frac{1}{2}$. Let's assign a number to X($\omega$). If we toss a coin and we get H, we receive 5 dollars, if we get T, we need to pay 5 dollars. So our event is as follows: $X(\omega) = 5 $ if $\omega$ = H and $X(\omega) = -5 $ if $\omega$ = T.

A stochastic process is a sequence of random variables. So let's define $X_t$, with t= Monday, Tuesday, Wednesday, Thursday, Friday, instead of t = 1,2,..,5.

1) We throw on Monday a coin and get H; we obtain 5, $X_{Monday}(\omega) = 5 $;

2) We throw on Tuesday a coin and get H; we obtain 5, $X_{Tuesday}(\omega) = 5 $;

3) We throw on Wednesday a coin and get T; we pay 5, $X_{Wednesday}(\omega) = -5 $;

4) We throw on Thursday a coin and get H; we obtain 5, $X_{Thursday}(\omega) = 5 $;

5) We throw on Friday a coin and get H; we obtain 5, $X_{Friday}(\omega) = 5 $;

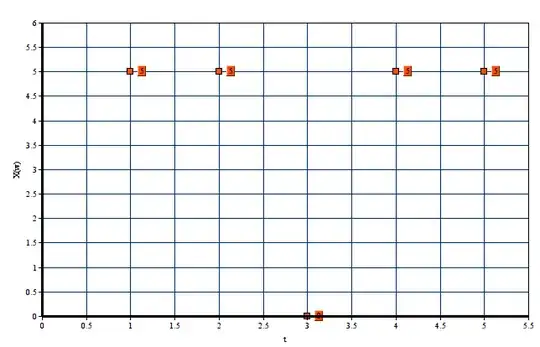
If we would graph this we get the following stochastic process:

enter image description here

I know the definition of a continuous function/process that is a sequence without any jump or holes, but I am not sure how to extend that idea to a right-continuous process. It makes intuitively just to think about that we fix $t$ at let's say Thursday, so t = 2 and then continue with the sequence up to Friday, so t = 5; we then have a right continuous sequence t = 2,...,5 but quite unsure about this.

My question is if someone can help me extend the example into a correct right continuous process and a left continuous process with a graph. Also, can someone tell me the intuition behind why we would need such a process? What does it tell us? Why is it useful?

Reference:

What is a right continuous(or left continuous ) stochastic process?

Probability Notation: What does $\{\omega\in \Omega : X(\omega) \in A\}$ mean?

An example of stochastic process

JayDough
  • 123
  • To meaningfully discuss a right-continuous process, you need to use continuous time. To extend your example, you might daily toss a coin at $12$ noon and win or lose $5$ depending on whether it is heads or tails. Suppose $t=0$ is Monday at $9$ am. Let $X_t$ be your total winnings after $t$ days, where $t$ is a continuous parameter. So, in particular, $t=1/8$ corresponds to Monday at $12$ noon. Then $X_t=0$ for $t<1/8$, but $X_{1/8}=5$ or $X_{1/8}=-5$ depending on the outcome of your coin. Then, $X_t$ once again remains constant until a day later. This is right- (but not left-) continuous. – Jason Apr 01 '20 at 15:03
  • Hey, can you explain where 1/8 comes from? – JayDough Apr 01 '20 at 15:31
  • The first toin coss is $3$ hours - or $1/8$ of a day - after time zero. – Jason Apr 01 '20 at 15:56
  • What's the intuition behind a right continuous process? – JayDough Apr 02 '20 at 07:45

0 Answers0