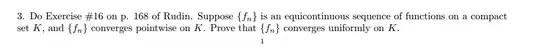0

Here is the definition I am given to equicontinuity:

enter image description here

I found this question here:

Is an equicontinuous family of uniformly continuous functions necessarily uniformly equicontinuous?

but I do not understand the definition of an equicontinuous family of continuous functions to be uniformly equicontinuous from it, could anyone tell me the definition of uniformly equicontinuous family of functions (in a way similar to the definition given above (without using small n)), please?

Now, I want to show that: an equicontinuous family of continuous functions on a compact metric space is uniformly equicontinuous.

And I found this question and its solution online:

enter image description here

enter image description here

And I found not less than 3 questions here on this site that answers a question similar to mine but not exactly mine(I have read them all), so could anyone help me proof this question: an equicontinuous family of continuous functions on a compact metric space is uniformly equicontinuous. and tell me how I will use compactness of the given metric space in the proof?

Community
  • 1
Emptymind
  • 2,217
  • Your 11.27 calls equicontinuous what the linked questions calls uniformly equicontinuous. The linked question calls equicontinuous a family of functions such that for all $x$ and $\varepsilon$ there is some $\delta$ such that, for all $f$ in the family and for all $y$ such that $d(x,y)<\delta$, $\lvert f(x)-f(y)\rvert<\varepsilon$. –  Mar 07 '20 at 17:23
  • ohh, but I have to answer the question based on my definition @Gae.S. so what is the definition of uniformly equicontinuous based on my definition? – Emptymind Mar 07 '20 at 17:28
  • Actually the exact definition for equicontinuity I was given is: A collection $\mathcal{F}$ of real-valued functions on a metric space $X$ is equicontinuous at $x \in X$ if $\forall \epsilon > 0, \exists \delta > 0,$ such that $\forall f \in \mathcal{F}, \forall x' \in X, $ we have $$\rho (x, x') < \delta \implies |f(x) - f(x')| < \epsilon $$ .... is this the same definition as the one given in 11.27 @Gae.S.? – Emptymind Mar 07 '20 at 17:36
  • 1
    If by equicontinuous you have been given "a family is equicontinuous if and only if it is equicontinuous at all points", then no, it isn't the same as 11.27. Personally, I'd call 11.27 uniformly equicontinuous. –  Mar 07 '20 at 17:44
  • yes the remainder of my definition(the definition I stated in my previous comment) is $\mathcal{F}$ is equicontinuous on $X$ if it is equicontinuous at every point of $X.$@Gae.S. – Emptymind Mar 07 '20 at 18:05

1 Answers1

2

See lemma 1 in my note here, which establishes this. The weaker notion is more pointwise; in its metric formulation:

$$\forall x\forall \varepsilon \exists \delta>0: \forall f \in \mathcal{F}: \forall y: (d(x,y) < \delta) \to \rho(f(x),f(y)) < \delta$$

so that we can find, given $x$,and $\varepsilon$, a $\delta$ that works for all functions at $x$, while the notion you defined is uses the same $\delta$ for all pairs $x,y$ and all $f$ at the same time. It's a similar difference between continuity at $x$ and uniform continuity.

You'll need to know the Lebesgue number lemma for the proof, as a basic fact about compact metric spaces.

Henno Brandsma
  • 250,824
  • Did you read the definition actually I have in my comments ? .... is it different from 11.27? – Emptymind Mar 07 '20 at 18:09
  • @Emptymind it's the same as my definition: you have equicontinuous at all $x$, while mine has the $\forall x$ at the beginning, same thing. It's the pointwise vs uniform gap. Bridged by compactness. 11.27 is my EQ2, yours from the comments or mine in in the answer is EQ1. – Henno Brandsma Mar 07 '20 at 18:11
  • Can not we interchange the usage of the Lebesgue number by an argument similar to the solution picture I attached above in the question? – Emptymind Mar 07 '20 at 19:46
  • @Emptymind You probably could, try to come up with one and post it as your own answer (this is the recommended way). – Henno Brandsma Mar 07 '20 at 19:50
  • Okay and I will ask you to see if it is correct or no ... ok? – Emptymind Mar 07 '20 at 19:58
  • @Emptymind sure, that way you learn the most. – Henno Brandsma Mar 07 '20 at 20:00
  • If you have time, could you look at this, please? https://math.stackexchange.com/questions/3573238/an-example-of-int-x-times-y-f-d-mu-times-lambda-is-finite-but-such-th – Emptymind Mar 08 '20 at 19:17