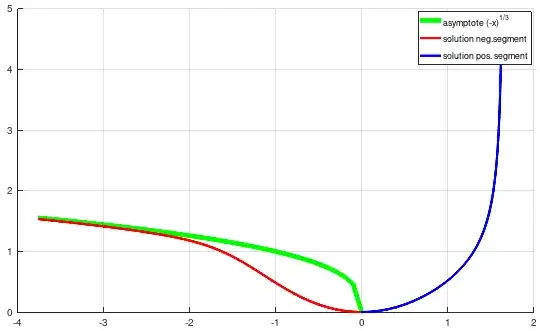
There's a Cauchy problem: $$ y'=x+y^3,\ \ y(0)=0 $$ Prove that there is a solution to this problem on the segment $\left[-\frac{1}{2},\frac{1}{2}\right]$
First, I tried to solve the given differential equation. But I got stuck, since the equation is non-linear. So, I thought that there must be a differet approach to this problem.
Could anyone give me a hint how I can deal with this task?
On the box $[-a,a]\times[-b,b]$, $a=\frac12$, the function value of the right side has a bound of $M=a+b^3$ and a Lipschitz constant $L=3b^2$.
The growth bound condition $Ma\le b$ and the contraction condition $La<1$, which written out are $$ \frac12+b^3\le 2b ~\text{ and }~ b^2<\frac23, $$ can be satisfied for $b=\frac13$. So indeed a solution exists on this interval.
This same method can be used to get larger intervals, $$ a^2+ab^3\le b\land 3ab^2\le 1 $$ can still be satisfied with $a=b=\frac23$.
The numerical solution shows a pole at about $x=1.6475$
