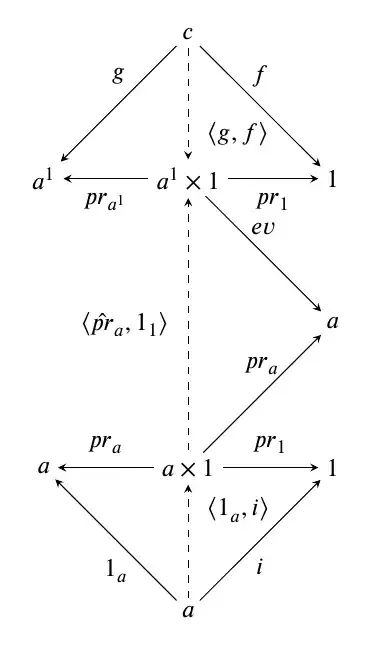
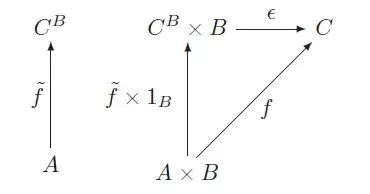
In Robet Goldblatt's 'The Categorial Analysis Of Logic', in section '3.16 Exponentiation', there is an exercise to prove that $a^1 \cong a$, and I have spent a while trying to get the right idea - which I suspect must be almost trivial, but it still eludes me. I am considering the following diagram:
Here I combine the diagrams for products of objects with the one for exponentiation (in the middle - I hope I've got them right), and that is where I'm stuck. I have chosen $pr_a \colon a \times 1 \rightarrow a$, which gives me $\hat{pr}_a \colon a \rightarrow a^1$, but how do I go the other way, so that I have an isomorphism?
Edit:
I don't think this is a duplicate - Goldblatt's book comes to this before mentioning Yoneda, so it should be possible to work this out using only Goldblatt's definition of exponentiation etc. I suspect that Yoneda may have followed a similar reasoning to get to the lemma.