3

A plane touches the globe at the north pole. A line through the south pole and through another point on the globe intersects that plane. That intersection point is the image, under the stereographic projection, of that other point on the globe than the south pole. The image of the south pole is the point at infinity in the one-point compactification of the plane.

It has long been known (for more than 2000 years, I think?) that

  • this mapping takes circles on the globe to circles on the plane, and
  • this mapping is conformal.

So my question is: What sorts of converses to this theorem are there?

And a secondary question: What is the history of this theorem and its converses and their proofs?

Michael Hardy
  • 1
  • 2
    It's an instructive exercise to calculate these things and show they hold. Here of course, circles on the plane must be considered as generalized circles (which include straight lines); either this, or one must consider only those circles on the globe that do not cross the point of projection. The stereographic projection can also be studied in the context of Mobious transformations which is a rich subject. – Fimpellizzeri Nov 22 '19 at 19:43
  • 2
    Question a bit vague! You have not phrased a specific "theorem" and it is not clear what your intended inverse should look like. Does it look like: If a map from a sphere to the plane does this and that then it is a stereographical projection (up to choice of south pole and origin)?" – Behnam Esmayli Dec 01 '19 at 14:03
  • @BehnamEsmayli : Yes, that is the question. $\qquad$ – Michael Hardy Dec 01 '19 at 14:13
  • I think that this is closely related. – Giuseppe Negro Dec 02 '19 at 09:11

1 Answers1

1

Answer to these questions can be found in the Wiki reference.

Since the projection mapping is bijective, circles on the plane ( of north -pole) map to circles on the globe when mapped from south pole as center for projection. An oblique cone with vertex at south pole cuts the sphere and a plane along these circles.

It is a conformal mapping. Angles are conserved but sense of rotation is reversed. Mapping of complex variables are all conformal.

If we plot the circles in Geogebra etc. it would be instructive. Begin with plotting of arbitrary curves by inversion in the plane ( plot them both) and then only proceed to stereographic 3D projection plotting. From similar triangles it is possible to derive all the transformation (mapping) formulas.

Latitudes/longitudes map as a polar grid and vice-versa.

However if you rotate the entire globe by $90^{\circ}$ maintaining tangent contact at a point on equator now making it new center of projection you obtain bipolar co-ordinate grid of orthogonal circles from lat/long circles... on a perpendicular plane containing both poles and center of sphere. The unit circle length appears in this projection interestingly at several places (power of circles, distance to concurrent points that are north/south pole ) images. This is also bijective.

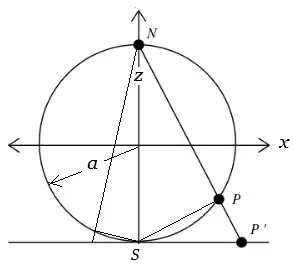
enter image description here

Let $\angle PNS = \theta$

From similar triangles $ NPS, NSP'$

$$ \rho = P'N=2a \sec \theta,\quad R= PN= 2a \cos \theta $$

$$ \rightarrow \rho \cdot R = 4 a^2 = 1,$$

if diameter $2a =1 $ for all $\theta.$

The projection holds for any figure on the sphere onto the plane.

To understand the phenomenon of projection the underlying bilinear Moebius complex variable mapping where circles map to circles is to be studied at first in 2D for effects of magnification, distortion and shift of the circles mapped: See e.g., at 31.00 in Balakrishnan Lecture

$$ w=\frac{az+b}{cz+d} $$

There is also an invariant Cross-ratio in the mapping.

Apart from this, fixed point referred to the given and mapped circles in stereographic projection can be identified as the north ( or south ) pole of sphere as the common vertex of oblique cone projection.

Wiki states that the projection was known from the first century, mostly due to need of astronomical body position studies. Mentioned in the modern form in Riemann's famous Habilitation lecture about Foundations of geometry.

Narasimham
  • 42,260
  • 1
    But I was asking about converses of these results, which would be characterizations, and thus would state that the stereographic projection is the ONLY projection possessing whichever properties the characterization states. – Michael Hardy Dec 02 '19 at 01:57
  • Yes agreed, it is true that astronomy since 2000 years had to wait for its key in Moebius transformation of the 18th century ! – Narasimham Dec 02 '19 at 08:54
  • While there are some interesting features in this answer, I don't see how it addresses the question. Also, I don't understand the reason of being harsh in some remarks, such as: "all your questions are already answered in wiki, your problem should be clearly stated, do you think it was a chance, etc..." – Giuseppe Negro Dec 02 '19 at 09:03
  • @Narasimham: there is no problem, that was obviously just a misunderstanding. Thank you for your comment. – Giuseppe Negro Dec 02 '19 at 09:26
  • @ Michael Hardy: I understood your question this way : Given circles C1,C2 in the basic 2D model or 3D stereographic projection model of inversion show that the operative is $ r→1/r $ from the center of projection. Ok? – Narasimham Dec 02 '19 at 09:34
  • @Narasimham : That was not the question at all. I used the words "converse" and "characterization" for a reason. – Michael Hardy Dec 02 '19 at 20:10