1

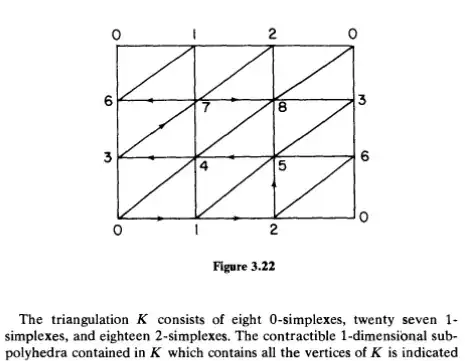
I stumbled upon the following triangulation of the Klein Bottle in page 76 of the book Topology and geometry for physicists by Charles Nash and Siddhartha Sen.

enter image description here

Below the figure, it says "the triangulation $K$ consists of eight $0$-simplexes[...]".

I think this is not an eight-vertex triangulation, but rather a nine-vertex triangulation of the Klein bottle. I also know, thanks to the great comments under this question, that an $8$-vertex triangulation of the Klein bottle is a minimal one, hence the one portrayed in the book isn't minimal.

Am I correct?

Whyka
  • 2,003
  • 2
    Note that the Euler characteristic of the Klein bottle is zero, so the numbers given for this illustration can't be right, since $8-27+18 \neq 0$. Indeed the 8 should be a 9. – John Palmieri Nov 12 '19 at 02:53
  • @JohnPalmieri That's a good point. Thank you – Whyka Nov 12 '19 at 03:02

1 Answers1

2

Yes, that is a nine-vertex triangulation: the vertices are in fact numbered for you: 0, 1, 2, ..., 8. You've pointed out this question, so I will add a link to the paper by Davide Cervone cited at that question, which gives a proof that there have to be at least 8 vertices, plus a classification of all 8-vertex triangulations.

John Palmieri
  • 9,136