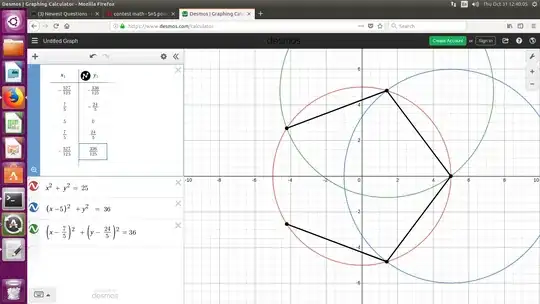
This is easier than it looks. All you need to do is use Pythagorean triples in the appropriate way.
Draw a circle with a diameter of five units. Select any point on the circle and generate other points from it by drawing chords with length three units joined end to end. All chords being congruent, they intercept congruent arcs and the arcs add together. Therefore the distance between any two points will have the form
$|5\sin(k\theta/2)|$
where $k$ is a whole number and $\theta$ is the minor arc intercepted by a chord. The multiple angle identities then guarantee that $\sin(k\theta/2)$ will be rational given the rational values $\sin(\theta/2)=3/5$ and $\cos(\theta/2)=4/5$. So all point-to-point distances are rational and they may be converted to integers by scaling appropriately. Since the value of $\theta$ as constructed here is not a rational number times $2\pi$, an unlimited number of distinct points may be identified, so there is no limit on $n$.