6

How to construct six points $ABCDEF$ on a plane so that the distance between any two of them is an integer, and no three are collinear?

I tried with some right angled triangles with pythagorean triples and you get 3 points. and i am stuck with 3 points

Batominovski
  • 50,341
endgame yourgame
  • 780
  • 7
    Note that you can get any finite number of points in the plane, each at integer distance from the others, no three collinear – see https://math.stackexchange.com/questions/3415894/n-points-on-a-circle-with-integer-distances To make the problem more interesting, it's usually required that no four points lie on a circle. This is harder. I'll find some references. – Gerry Myerson Apr 28 '20 at 11:30
  • 5
    Tobias Kreisel and Sascha Kurz, There are integral heptagons, no three points on a line, no four on a circle, Discrete Comput. Geom. 39 (2008), no. 4, 786–790, MR2413160 (2009d:52021) – Gerry Myerson Apr 28 '20 at 11:33

2 Answers2

9

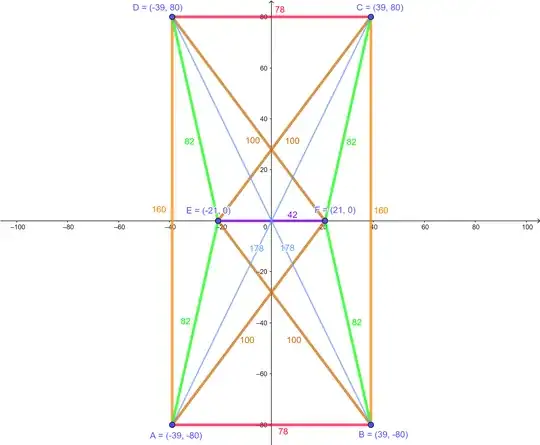
See the attached image. The idea is to find Pythagorean triples $(a,b,c)$, $(a,d,e)$, and $(2a,b+d,f)$ such that $b<d$. Then, let $$A=(-b-d,-2a),$$ $$B=(b+d,-2a),$$ $$C=(b+d,2a),$$ $$D=(-b-d,2a),$$ $$E=(b-d,0),$$ and $$F=(-b+d,0).$$ Therefore, $$AB=CD=2(b+d),$$ $$BC=DA=4a,$$ $$AC=BD=2f,$$ $$EA=ED=FB=FC=2c,$$ $$EB=EC=FA=FB=2e,$$ and $$EF=2(d-b).$$ I found $(a,b,c)=(40,9,41)$, $(a,d,e)=(40,30,50)$, and $(2a,b+d,f)=(80,39,89)$.

enter image description here

If you want a convex hexagon, you can find Pythagorean triples $(a,b,c)$, $(a,d,e)$, and $(2a,d-b,f)$ such that $b<d$. Then, let $$A=(b-d,-2a),$$ $$B=(-b+d,-2a),$$ $$C=(-b+d,2a),$$ $$D=(b-d,2a),$$ $$E=(-b-d,0),$$ and $$F=(b+d,0).$$ Therefore, $$AB=CD=2(d-b),$$ $$BC=DA=4a,$$ $$AC=BD=2f,$$ $$EA=ED=FB=FC=2c,$$ $$EB=EC=FA=FB=2e,$$ and $$EF=2(b+d).$$ I found $(a,b,c)=(12,9,15)$, $(a,d,e)=(12,16,20)$, and $(2a,d-b,f)=(24,7,25)$. See the image below.

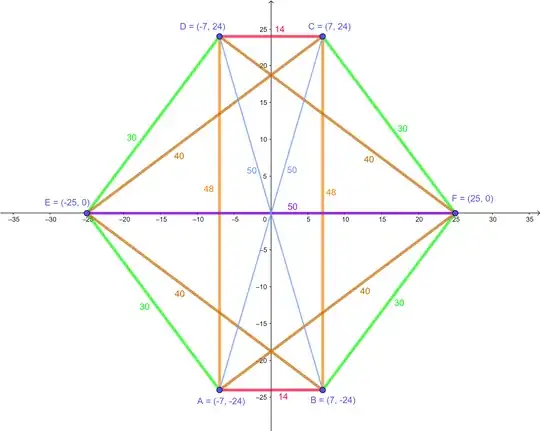
enter image description here

The last picture is very nice. This hexagon is also inscribed in a circle with integer radius. However, $AC$, $BD$, and $EF$ are all diameters of this circle. This makes me think: is it possible to find a cyclic hexagon $ABCDEF$ such that all sides and diagonals have integer lengths, the circumradius is also an integer, and no diagonal or side of the hexagon is a diameter of the circumcircle?

Batominovski
  • 50,341
  • 1
    In reponse to that last question: The answers to https://math.stackexchange.com/questions/3415894/n-points-on-a-circle-with-integer-distances guarantee that such a cyclic polygon always exists, with any number of sides. This solution is somewhat inelegant, however, as the size of the circle would have to increase exponentially with the number of polygonal sides. – Oscar Lanzi Apr 28 '20 at 17:48
  • Re your last question, on a circle of radius $65/2$, we may take points which, by threes, make triangles with the following side lengths (many copies of each shape): 39,25,16; 52,33,25; 56,39,25; 60,39,33; 60,52,16; 60,56,52; 63,52,25; 63,60,39. Unfortunately, each point comes with its diametrically opposite point. However, there are so many points that it should be possible to pick 6 and avoid diametrically opposite pairs, e.g. those on one semicircle. Now double all lengths to make the radius 65. – Rosie F Jan 14 '23 at 10:23
0

The OP does not impose any upper bound on how many of the points may be on the same circle, or any requirement that their Cartesian coordinates must be integer (or even rational). So let me offer an alternative approach: all the points are on a circle of radius $R=n/\sqrt3$ where $n$ is a Loeschian number with $3\nmid n$. For example, we may take $n=7, R=7/\sqrt3$.

The distances between the points are $AB=CD=EF=3$; $BC=DE=FA=5$; $AC=CE=EA=BD=DF=FB=7$; $AD=BE=CF=8$.

We may construct configurations of even more concyclic points at integer distances by taking $n$ as the product of $k$ distinct primes $p_i=1\mod 6$. The greater $k$, the more points.

Cyclic hexagon, sides length 3, 5; diagonals length 7, 8

Rosie F
  • 3,231