Why is the "Power of a Point" of an Internal Point on a Circle Negative?

Question

The Wikipedia Article on Power of a Circle gives the following explanation:

In elementary plane geometry, the power of a point is a real number $h$ that reflects the relative distance of a given point from a given circle. Specifically, the power of a point P with respect to a circle O of radius $r$ is defined by (Figure 1).

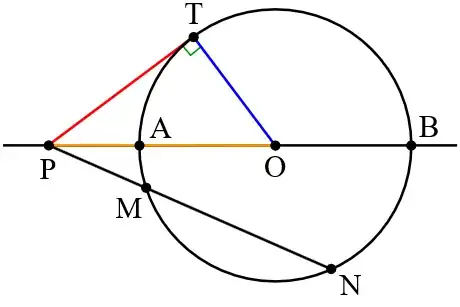
Figure 1. Illustration of the power of point P in the circle centered on the point O. The distance s is shown in orange, the radius r is shown in blue, and the tangent line segment PT is shown in red.

$h=s^{2}-r^{2}$

where $s$ is the distance between P and the center O of the circle. By this definition, points inside the circle have negative power, points outside have positive power, and points on the circle have zero power. For external points, the power equals the square of the length of a tangent from the point to the circle. The power of a point is also known as the point's circle power or the power of a circle with respect to the point.

I am unable to understand, how to conclude that the power of an internal point is negative, from the definition. Power is actually square of the length of tangent. I can understand it is positive and zero for points outside and on the circle. Only thing, I can think of internal points is their length is imaginary and so their square is negative. Is this reasoning correct? Are there any other explanations on why is the power of internal points negative? If so, kindly explain them.

Further, is this in anyway related to the following fact which I learnt previously?:

Let us consider a circle, $x^2+y^2+2gx+2fy+c=0$. The point $(h,k)$ lies outside, on or inside the circle accordingly as $h^2+k^2+2gh+2fk+c$ is positive, zero or negative.

Answer 1

As a first pass at the notion, you could say that signed powers are simply a convention that we accept from the relation $h=s^2-r^2$. (It's worth noting that people sometimes neglect to refer to "inside" powers as negative. I've probably done this a few times when I'm discussing something happening specifically inside the circle, and the sign would be a distraction.)

That said, signed powers are important for defining, say, the "radical axis" of two circles: points whose powers with respect to the circles are equal. (Conveniently, for circles with equations $(x-h)^2+(y-k)^2=r^2$ and $(x-p)^2+(x-q)^2=s^2$, the equation of the radical axis arises from subtracting one equation from another. Proving this is a nice little exercise.)

Here's a possibly-helpful way of thinking about this: Consider point $P$ and circle $\omega$. Draw any line through $P$ that meets $\omega$, and let these points of intersection be $A$ and $B$ (where $A=B$ in the case of tangency). It happens that, whatever line you draw, the product $|PA||PB|$ always yields the same number (this is the Power of a Point Theorem); the power of $P$ is that product, except we take it to be positive when $\overrightarrow{PA}$ and $\overrightarrow{PB}$ point the same direction (equivalently, when $P$ is outside the circle), and negative if they point in opposite directions (when $P$ is inside). For $P$ on the circle, the product is zero, so it doesn't matter which sign convention you use.

(The above has a subtle, satisfying consistency with signed ratios we see in, for instance, Ceva's Theorem and Menelaus' Theorem.)

In any case, the notion of signed powers can seem a little weird at first, but it does come in handy.

---

As to your question about the inside-ness test of $(h,k)$ relative to the circle with equation $x^2+y^2+2gx+2fy+c=0$: Yes, the notions are related.

We can write the circle equation as $$(x-g)^2+(y-f)^2-r^2=0 \qquad \text{where}\; r^2 = f^2+g^2-c$$ so that we identify the circle's center $K=(g,f)$ and radius $r$.

But note that $(x-g)^2+(y-f)^2$ gives the distance from point $P=(x,y)$ to $K$. That is, we have $$|PK|^2-r^2=0$$ The left-hand side is exactly the definition of the power of $P$ with respect to the circle; but the right-hand side is just a re-written version of the left-hand side of the original equation.

Therefore, $x^2+y^2+2gx+2yf+c$ is itself really just the power calculation, which is why the inside-ness test works as you described.

Answer 2

Let's consider an example with the unit circle (radius 1, centered at the origin). So, the power of $(2,0)$ is $2^2-1^2=3$ and the power of $(\frac12,0)$ is $\left(\frac12\right)^2-1^2=-\frac34$. Of course, there is no tangent line to the circle that goes through $(\frac12,0)$ -- any line that goes through the interior of the circle has to be a secant. To me, thinking about the length of the tangent to that circle as $\frac{i\sqrt3}{2}$ is as mind-warping as thinking that the parabola $y=x^2+1$ actually crosses the x-axis at $\pm i$.

For your last question, yes. If you squeeze that equation into the form $(x-x_0)^2+(y-y_0)^2=r^2$, and then work out the distance from $(x_0,y_0)$ to $(h,k)$, I have every confidence that the equation would balance out as they presented it.