The problem is stated as a global optimization (maximize the probability of finding the ball in no more than $k$ attempts), but it seems true (assumed, not proved here [*]) that it's equivalent to iteratively (greedily) maximize the probability of finding the ball in the next attempt.
Let $c_i$ be the probability of finding the white ball when attempting an extraction from bag $i$, conditioned that the white ball is there. This doesn't change.
Let $X$ be the position of the ball, and let $p_i=P(X=i)$ be the probability of the white ball being in bag $i$. Initially, this is a given priori. At each (failed) attempt, we'll update this to reflect the a posteriori probability.
Let $F_i$ be the event that we failed to get the white ball, given we tried bag $i$.
To maximize the probability of success on the first attempt, is to mimimize $F_i$. But $P(F_i) = 1 - d_i$, where $d_i = p_i \, c_i$. Hence, denoting by $s$ the selected bag, we have $s= \mathrm{argmax}_i \, d_i$ . And the probability of success is $d_s=\max_i(d_i)$
Given that we failed, the probabilities $p_i$ are updated via Bayes thus:
For $i=s$:
$$
\begin{align}
p'_s=P(X=s \mid F_s)&=\frac{P(F_s\mid X=s)P(X=s)}{P(F_s\mid X=s)P(X=s)+P(F_s\mid x\ne s)P(X\ne s)}\\
&=\frac{(1-c_s)p_s}{(1-c_s)p_s + (1-p_s)}\\
&=\frac{p_s-d_s}{1-d_s} \tag 1
\end{align}$$
For $i\ne s$ we first compute
$$
\begin{align}
P(F_s \mid X \ne i) &= P(F_s \mid X=s, X \ne i ) P(X=s\mid X \ne i) + P(F_s \mid X \ne s, X \ne i)P(X=s\mid X \ne i) \\
&= (1-c_s) \frac{p_s}{1-p_i} + 1\times (1 - \frac{p_s}{1-p_i}) \\
&= \frac{1}{1-p_i}(1- p_i - c_s p_s)
\end{align}
$$
And then
$$
\begin{align}
p'_i =P(X=i \mid F_s)&= \frac{P(F_s\mid X=i)P(X=i)}{P(F_s\mid X=i)P(X=i)+P(F_s\mid X\ne i)P(X\ne i)} \\
&= \frac{ 1\times p_i }{1\times p_i + \frac{1}{1-p_i}(1- p_i - c_s p_s) (1-p_i) }\\
&=\frac{p_i}{1 -c_s p_s} = \frac{p_i}{1 - d_s} \tag{2}
\end{align}$$
With $(1)$ and $(2)$ together we update the probabilites $p_i$ and $d_i$ and repeat.
An example with $n=4$ bags and $k=5$
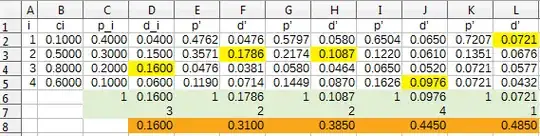
In yellow, the selected bags in each attempt. In orange, the probability of having found the white ball at that point.
Update: For large $k$ , we could attempt a maximization using (abusing) Lagrange multipliers.
I'll spare the details (ask if you want them), but the result is
Let $k_i$ denote how many times bag $i$ was selected, in $k$ extractions (hence $\sum_{i=1}^n k_i=k$)
Then the probability of failure is
$$\begin{align} P(F; k_1,k_2 \cdots k_n) &= \sum_{i=1}^n P(X=i) P(F \mid X=i; k_1,k_2 \cdots k_n) \\
&= \sum_{i=1}^n p_i (1 - c_i)^{k_i}
= \sum_{i=1}^n p_i e^{ -a_i \,k_i}
\end{align}$$
where $a_i = - \log(1-c_i)$
We wish to minimize this function of the multivariate variable $(k_1,k_2 \cdots k_n)$ subject to the condition $C(k_1,k_2 \cdots k_n) = \sum_{i=1}^n k_i-k =0$
Lagrange multipliers would be apt for this.. except that our variables are not real but integer. Anyway, abusing the method, equating the derivative to zero gives:
$$ - p_i a_i e^{ -a_i \,k_i} + \lambda = 0 \hskip{1 cm} i=1,2 \dots n$$
which can be written as
$$k_i = \frac{\log(\, p_i a_i) + \beta }{a_i} \tag 3$$
where and $\beta$ is a number that is obtained by solving (numerically, it seems) the constraint $\sum k_i = k$ together with $(3)$.
Of course, $(3)$ gives non integer numbers, we should expect that rounding to the nearest integers (always respecting the sum restriction) gives at least a good approximation to the optimal value.
For example, with $k=10$ and same $p_i$, $c_i$ as in the example above, I get $k_i=(4.198, 2.941, 1.538, 1.330)$ while the optimal values are $(4, 3, 2 ,1)$.
