1

enter image description hereDoes anyone know how to formulate a set of parametric equations that generate an egg-shape?

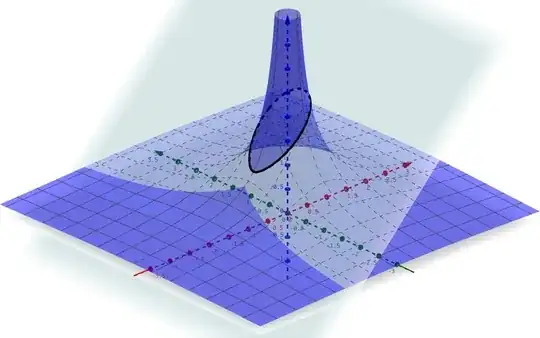
NOTE. I've asked several people, including my calculus professor, and in every case, what I got were variations on the standard, symmetrical ellipse. What I want can be defined in a few ways; a form whose curvature is a combination of two or more different ellipses. Or, an egg-shaped section from a 3-d hyperbolic form, i.e., revolve:

$$y=\frac{1}{x}$$

then cut it at an angle yielding an egg-form.

Thank you for your time!

NOTE. See fig.

For My Example

$$y=\frac{1}{x}$$

$$y=x-2.02$$

Both on the same plane.

Lee Mosher
  • 135,265
Jinny Ecckle
  • 73
  • 1
  • 13
  • If anyone doesn't get what I mean with the hyperbolic shape, I can do it in solid works and show you; feel free to ask. – Jinny Ecckle Sep 30 '19 at 18:41
  • "If anyone doesn't get what I mean with the hyperbolic shape, I can do it in solid works and show you; feel free to ask." ... I'm asking. :) – Blue Sep 30 '19 at 18:42
  • 1
    This is an old question. – Dietrich Burde Sep 30 '19 at 18:42
  • 1
    With a bit of intentional sarcasm - this is probably going to be closed due to lack of precision. Which egg? Chicken? Duck? Shark? –  Sep 30 '19 at 18:42
  • A similar question is here. – Dietrich Burde Sep 30 '19 at 18:43
  • Any egg-shap that is a-symmetrical above and beneath the y axis. – Jinny Ecckle Sep 30 '19 at 18:44
  • @JinnyEcckle An intersection of a quadratic surface with a plane is always one of the conic sections - so you probably still end up with an oval if you do it. –  Sep 30 '19 at 18:44
  • @StinkingBishop I've done this before, so, I can prove it. Give me a few min! – Jinny Ecckle Sep 30 '19 at 18:45
  • Your title says "true egg shape", but your description asks to combine curves that arguably won't provide a "true egg shape". I guess it depends upon your definition of "true". ... In any case, have you searched Math.SE for "egg"? For instance, there's this. – Blue Sep 30 '19 at 18:49
  • See also https://math.stackexchange.com/a/407454/856, http://www.mathematische-basteleien.de/eggcurves.htm, https://www.mathcurve.com/courbes2d.gb/oeuf/oeuf.shtml. –  Sep 30 '19 at 19:02
  • To all who doubted what I said, see my image (now in the post). – Jinny Ecckle Sep 30 '19 at 19:21
  • @Blue, sorry for the slight lack of rigor; I meant far more true than what I was given. Ideally, it would be a perfect form; but certainly I'd like something better than what I've been given before.... – Jinny Ecckle Sep 30 '19 at 19:32
  • @StinkingBishop I posted it in my post; so you can see it for yourself.... – Jinny Ecckle Sep 30 '19 at 19:33
  • To all; in my experience, you can get nearly any egg-shape in the way shown in my photo. The one given is a point-y chicken-egg shape, as seen from some heirloom hens (yes, I've measured this LOL). – Jinny Ecckle Sep 30 '19 at 19:35
  • Netwon's egg $y^2 = (x^2-1)(x-a)$, $(a \sim 3)$, Cubic egg $x^2 + y^2(1+ax) = 1$, $(a < 1)$, Wassenaar (egg) $(y-x^2)^2 = 1-ax^2$, $(a \sim 5)$.... – achille hui Sep 30 '19 at 19:42
  • There is no true (chicken) egg shape afik . Inversions of some eccentric ellipses about a circle contour when used as circle of inversion produce egg profiles of reasonably accurate shape... imho. – Narasimham Oct 01 '19 at 05:58
  • @Narasimham The validity of your statement depends on whether or not on is a Platonist...... – Jinny Ecckle Oct 01 '19 at 14:36

1 Answers1

2

Intersecting the surface $z=1/\sqrt{x^2+y^2}$ with a plane $z=kx+b$ gives a curve in 3-space. Rotating this curve by $\arctan k$ about the $y$-axis gives a curve in a plane parallel to $(xy)$-plane, having parametric equations (for $b^2\ge4k$): $$ \begin{align} &x={1\over2\sqrt{1+k^2}} \left({k^2-1\over k}b+{k^2+1\over k}\sqrt{b^2-4k\cos t}\right)\\ \\ &y={2\sin t\over b+\sqrt{b^2-4k\cos t}}\\ \end{align} $$ This can give an egg shape for suitable values of $b$ and $k$. Here's the result for $k=1$ and $b=2.02$:

enter image description here

enter image description here

Intelligenti pauca
  • 55,765
  • 1
    Sorry for not responding sooner. This is absolutely brilliant! And, seeing what and how you did this will make this subject very cool to play around with. Seeing that you're a physics guy, I see why you got what I meant.

    Lovely, elegant work!

     – Jinny Ecckle Oct 01 '19 at 14:39