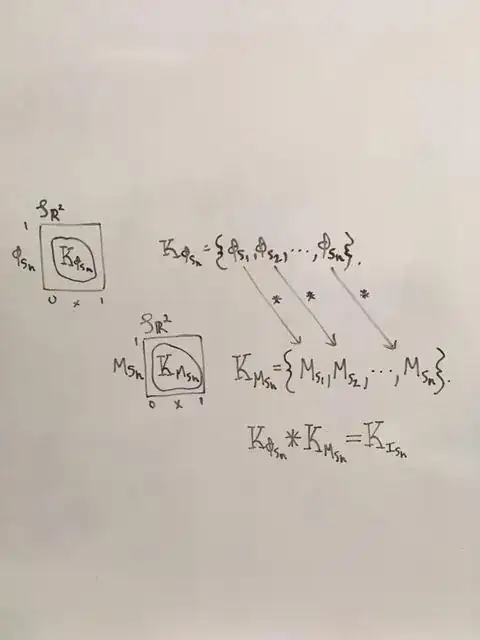Assume that there are two manifolds $K_{M_{S_n}}$ and $K_{\Phi_{S_n}}$ $\in (0,1)^2$ that are comprised of trajectories that points flow across, from $(0,1)$ and $(0,0)$ to $(1,0)$ and $(1,1)$ respectively. Assume each manifold is the same dimension and that each manifold is endowed with a hyperbolic structure, s.t. a stable horocyclic flow can be defined on each of them. Assume also that each manifold is a class of real analytic functions, and that all points flowing across the manifolds exit the source(s) at the same time, and enter the sink(s) at the same time. I think this last statement means the speed of the flows should be proportional to the the derivatives of the curves, evaluated along lines of the form $y=x\pm b$ (for $K_M$) and $y=-x\pm b$ (for $K_\Phi$).
Some context: Geometry of transformed spacetimes?, Lifting class structures from a lorentzian manifold $\Bbb R^{1,1}$ to $\Bbb R^{1,2}$.
Q1: If one defines a component-wise binary operation (convolution) on the functional elements comprising the stable manifolds $K_{M_{S_n}} \star K_{\Phi_{S_n}} = K_{I_{S_n}},$ to produce another manifold with hyperbolic structure, does $K_{I_{S_n}}$ also admit a stable horocyclic flow?
Edit: Here is my desmos code of the construction: Desmos Code.
Q2: Do complex structures on these three, real-analytic manifolds exist, and are they unique?
A schematic diagram of the manifolds expanded into their $n$-dimensional representations, in which each element in the set is a trajectory, or one-dimensional manifold.