If you have a square grid, and each square* has probability $n$ of being ground. If the other squares are water, what is the average area of an island? If $n$ is small then the average island would have an area of about $1$. With large values of $n$, the average size of islands is really big. Also diagonally touching squares don’t count as being the same island. Unless of course they connect somewhere else. *Each with an area of $1$.
-
2What exactly are you asking here, and what work have you done on it? – DanLewis3264 Jul 10 '19 at 23:58
-
1If you have an "island" with water in the middle, for example a $3\times 3$ square of ground tiles without the center tile, do you consider the center to be a part of the area or no? – JMoravitz Jul 11 '19 at 00:03
-
1Do you consider two land squares that touch only in a corner to be the same island, or two separate islands? – Arthur Jul 11 '19 at 00:06
-
I would assume this to be the correct interpretation of the problem. Rephrased in terms of graph theory, letting each location on the $n\times n$ grid be represented by a possible vertex, and a vertex appearing in an available position with probability $p$ independently at random from all other possible vertices, edges defined between vertices if their positions are adjacent in the grid, the question is what the expected value of the ratio of number of present vertices is over the number of connected components. Seems like a horribly difficult problem. – JMoravitz Jul 11 '19 at 00:11
-
2@JMoravitz, Indeed, the model you mentioned is one of the main object in the area called percolation theory. Considering the square lattice $\mathbb{Z}^2$ and the connected component $\mathcal{C}$ around $0$, it is proved that there exists $p_c \in (0, 1)$ for which the followings hold: $\mathbb{E}[|C|]<\infty$ if and only if $p<p_c$. I am not sure which model OP is exactly referring to, but I am fairly certain that it lies within the purview of percolation theory and that it is very hard. – Sangchul Lee Jul 11 '19 at 00:27
-
What does "square*" mean? – Cameron Buie Jul 11 '19 at 00:28
-
The * indicates that there is a footnote. In this case it mentions that the area of a square is 1. – Q the Platypus Jul 11 '19 at 01:00
1 Answers
I did an experiment with some Java code.
- I have checked all probabilities, starting from 5% in steps of 2.5% up to 100%.
- Each experiment is repeated 500 times before the average island size is calculated.
- The size of the "sea" is $50\times50$
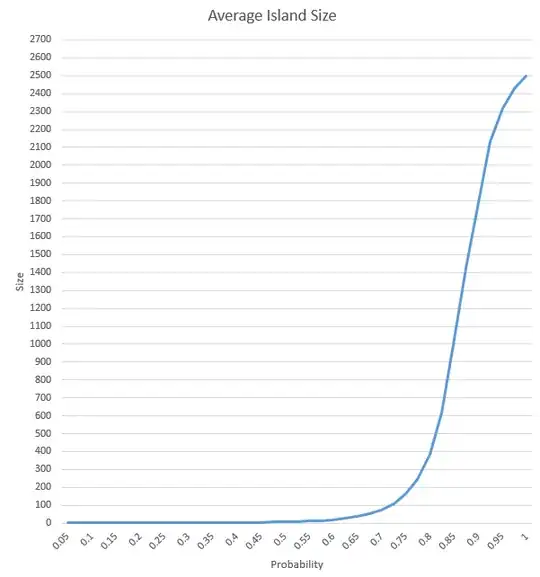
Here are the results:
$$ \begin{array}{l|l} \text{Probability} & \text{Average Island Size} \\ 0.050000 & 1.108420 \\ 0.075000 & 1.171769 \\ 0.100000 & 1.239889 \\ 0.125000 & 1.322296 \\ 0.150000 & 1.409073 \\ 0.175000 & 1.509786 \\ 0.200000 & 1.627313 \\ 0.225000 & 1.756252 \\ 0.250000 & 1.904399 \\ 0.275000 & 2.080445 \\ 0.300000 & 2.295080 \\ 0.325000 & 2.528017 \\ 0.350000 & 2.823988 \\ 0.375000 & 3.180992 \\ 0.400000 & 3.618721 \\ 0.425000 & 4.142728 \\ 0.450000 & 4.827669 \\ 0.475000 & 5.725215 \\ 0.500000 & 6.911376 \\ 0.525000 & 8.596760 \\ 0.550000 & 10.841804 \\ 0.575000 & 14.148635 \\ 0.600000 & 18.840807 \\ 0.625000 & 26.346250 \\ 0.650000 & 35.965670 \\ 0.675000 & 50.930806 \\ 0.700000 & 73.566788 \\ 0.725000 & 106.523051 \\ 0.750000 & 161.343357 \\ 0.775000 & 242.921195 \\ 0.800000 & 383.797845 \\ 0.825000 & 613.803805 \\ 0.850000 & 1026.555037 \\ 0.875000 & 1425.019748 \\ 0.900000 & 1789.621500 \\ 0.925000 & 2132.510333 \\ 0.950000 & 2316.020000 \\ 0.975000 & 2427.573000 \\ 1.000000 & 2500.000000 \end{array} $$
It seems that the average size of the island starts to grow rapidly for $p\gt0.65$.
And here is the code if you want to check it for correctness:
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Random;
public class IslandMap {
public static final int SEA_SIZE = 100;
public static final int NUM_EXPERIMENTS = 500;
public static final double PROBABILITY_INCREMENT_PCT = 2.5;
public static final double START_PROBABILITY_PCT = 5.0;
private static Random rnd = new Random(System.currentTimeMillis());
private List<Island> islands;
private double probability;
public static void main(String[] args) {
System.out.println("Probability,AvgSize");
for (double prob = START_PROBABILITY_PCT; prob <= 100D; prob += PROBABILITY_INCREMENT_PCT) {
Stats stats = new Stats();
for (int i = 0; i < NUM_EXPERIMENTS; i++) {
IslandMap map = new IslandMap(prob / 100D);
map.createIslands();
while (map.mergeIslands()) {
// NOP
}
double[] results = map.getStats();
stats.accum(results);
}
String msg = String.format("%f,%f", prob / 100D, stats.getAvgAvg());
System.out.println(msg);
}
}
IslandMap(double probability) {
this.probability = probability;
}
List<Island> createIslands() {
islands = new LinkedList<Island>();
for (int i = 0; i < SEA_SIZE; i++) {
for (int j = 0; j < SEA_SIZE; j++) {
if (rnd.nextDouble() <= probability) {
Square s = new Square(i, j);
islands.add(new Island(s));
}
}
}
return islands;
}
boolean contains(Square s) {
for (Island island : islands) {
if (island.contains(s)) {
return true;
}
}
return false;
}
boolean mergeIslands() {
boolean changed = false;
int i = 0;
while (i < islands.size() - 1) {
int j = i + 1;
while (j < islands.size()) {
boolean joined = islands.get(i).merge(islands.get(j));
if (joined) {
changed = true;
islands.remove(j);
} else {
j++;
}
}
i++;
}
return changed;
}
double[] getStats() {
int minSize = SEA_SIZE * SEA_SIZE;
int maxSize = 0;
int totalSize = 0;
for (Island island : islands) {
minSize = Math.min(minSize, island.size());
maxSize = Math.max(maxSize, island.size());
totalSize += island.size();
}
double avgSize = (double) totalSize / (double) islands.size();
double[] result = new double[] { minSize, maxSize, avgSize };
return result;
}
}
class Island {
private List<Square> squares = new ArrayList<Square>();
Island(Square s) {
squares.add(s);
}
boolean contains(Square s) {
return squares.contains(s);
}
boolean merge(Island island) {
for (Square s1 : squares) {
for (Square s2 : island.squares) {
if ((s1.x == s2.x && Math.abs(s1.y - s2.y) == 1) || (s1.y == s2.y && Math.abs(s1.x - s2.x) == 1)) {
squares.addAll(island.squares);
return true;
}
}
}
return false;
}
int size() {
return squares.size();
}
@Override
public String toString() {
StringBuffer b = new StringBuffer("");
b.append("SIZE: ").append(size());
for (Square s : squares) {
b.append(": (").append(s.x).append(",").append(s.y).append(") ");
}
return b.toString();
}
}
class Square {
int x, y;
Square(int x, int y) {
this.x = x;
this.y = y;
}
@Override
public boolean equals(Object obj) {
// TODO Auto-generated method stub
Square s = (Square) obj;
return x == s.x && y == s.y;
}
}
class Stats {
private double[] stats = new double[3];
private int count;
void accum(double[] stats) {
this.stats[0] += stats[0];
this.stats[1] += stats[1];
this.stats[2] += stats[2];
count++;
}
double getAvgMin() {
return stats[0] / count;
}
double getAvgMax() {
return stats[1] / count;
}
double getAvgAvg() {
return stats[2] / count;
}
}
I'm currently running the same simulation for the sea of size $100\times100$. It will take much, much more time but I still expect to get the curve of the same shape.
- 17,264