Calculate circle radius with given triangle

Question

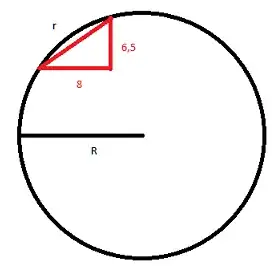
The following information is given:

Given the legs of red triangle, find R. Little 'r' is the length of the arc between 2 red intersections with circle. It is unknown. Is that possible or the task is not defined correctly ?

Is r meant to to be the same length as R? If so that is most likely solvable, but if not then the question needs more information. — W M Seath, May 23 '19 at 14:53
If $r$ is that arc of the circle and is given, it is possible, I think. — Paulo Mourão, May 23 '19 at 14:54
Every sufficiently large circle contains that right triangle. — lulu, May 23 '19 at 14:54
Welcome to Mathematics Stack Exchange! A quick tour will enhance your experience. Here are helpful tips to write a good question and write a good answer. For equations, please use MathJax. — dantopa, May 23 '19 at 14:57

score 1 · Answer 1 · answered May 23 '19 at 17:31

If we know the lengths of chord and arc then it is possible. The length of the chord is $d=\sqrt{8^2+6,5^2} \approx 10.31$. Now if we connect ends of the chord with the center of the circle, we will get a sector which has a measure $\theta$. We know that $\theta=\frac{r}{R}$. Thus we have an isosceles triangle formed by two radii and the chord which has vertex angle $\theta$. Draw a height from the center of the circle, the height will be a median and a bisector. This gives us another equation: $\sin \frac{\theta}{2}=\frac{d}{2R}$ or $$\color{blue}{\sin \frac{r}{2R}=\frac{d}{2R}}$$ This equation has one unknown and can be solved using numerical methods.

Thanks :), I will have to try this if other methods fail. Arc is unknown :S — Roland, May 23 '19 at 20:59
@Roland: Welcome! Now you see that if $r$ is the second unknown, you have unlimited number of solutions for $R$ so you need a second equation or more data. — Vasili, May 23 '19 at 21:10

score 0 · Answer 2 · answered May 23 '19 at 16:58

0

Friend linked this answer to me: Calculate the radius of a circle given the chord length and height of a segment

It should work provided we move the red triangle a little

answered May 23 '19 at 16:58

Roland

101

How are you going to measure the height of the segment? – user May 24 '19 at 09:09
In the link I pasted, the triangle PXV is my triangle, it seems. – Roland May 24 '19 at 22:12
The link has nothing to do with measurements. – user May 25 '19 at 14:11
If you move the triangle so one leg aligns with radius, you can calculate using the formula in the link above. – Roland May 26 '19 at 01:40
On the one hand you cannot align the triangle with radius, and on the other hand you cannot use the formula. If you disagree describe the exact procedure in your answer not in a comment. – user May 26 '19 at 06:31
Why I cannot move the triangle ? – Roland May 27 '19 at 15:38
You can. But it does not tell you where is the center of the circle. – user May 27 '19 at 16:09

score 0 · Answer 3 · answered May 24 '19 at 07:21

Starting from @Vasya's answer $$\sin \left(\frac{r}{2 R}\right)=\frac{d}{2R}$$ let $x=\frac{r}{2 R}$ and $k=\frac d r$ to make $$\sin(x)=k x$$ which does not make any problem as long as $k<1$. Newton method would probably be the simplest to use.

You can have a very good approximation of $x$ using $$\sin(x) \simeq \frac{16 (\pi -x) x}{5 \pi ^2-4 (\pi -x) x}\qquad (0\leq x\leq\pi)$$ proposed by Mahabhaskariya of Bhaskara I, a seventh-century Indian mathematician. Using it, you are left with the quadratic equation $$4 k x^2+(16-4 \pi k) x+\pi (5 \pi k-16)=0 \implies x=\frac{2 \sqrt{-\pi ^2 k^2+2 \pi k+4}+\pi k-4}{2 k}$$ For illustration purposes, $$\left( \begin{array}{ccc} k & \text{approximation} & \text{exact} \\ 0.05 & 2.99294 & 2.99146 \\ 0.10 & 2.85371 & 2.85234 \\ 0.15 & 2.72180 & 2.72114 \\ 0.20 & 2.59560 & 2.59574 \\ 0.25 & 2.47378 & 2.47458 \\ 0.30 & 2.35522 & 2.35644 \\ 0.35 & 2.23894 & 2.24033 \\ 0.40 & 2.12403 & 2.12535 \\ 0.45 & 2.00960 & 2.01067 \\ 0.50 & 1.89477 & 1.89549 \\ 0.55 & 1.77859 & 1.77894 \\ 0.60 & 1.65996 & 1.66003 \\ 0.65 & 1.53760 & 1.53761 \\ 0.70 & 1.40988 & 1.41019 \\ 0.75 & 1.27459 & 1.27570 \\ 0.80 & 1.12856 & 1.13110 \\ 0.85 & 0.96677 & 0.97135 \\ 0.90 & 0.78035 & 0.78668 \\ 0.95 & 0.55016 & 0.55191 \end{array} \right)$$

score -1 · Answer 4 · answered May 23 '19 at 15:15

-1

Assuming $r$ is the length of that arc and that it's given, then it is possible. Otherwise it isn't, since then you can make $R$ arbitrarily large.

answered May 23 '19 at 15:15

Paulo Mourão

1,774

Calculate circle radius with given triangle

4 Answers4