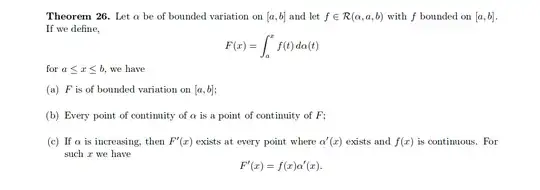This is a well known result of Riemann Stieltjes integration:
All the proofs I found use the fact that $f$ is bounded and apply one the Mean Value Theorem Riemann-Stieltjes Integrals (this one). I also found this problem without the assumption of $f$ bounded on $[a,b]$. Is it possible to prove this result without assuming the boundedness of $f$ ? I believe that the fact of $f$ being Riemann stieltjes integrable implies $f$ is bounded too. Thanks in advance.
In view of the definition of what it means to be Riemann-Stieltjes integrable, it is necessary that the integrand $f$ be bounded.
When the integrator $\alpha$ is monotone, the definition of the integral can be based on upper and lower Darboux-type sums, but these are clearly ill-defined when $f$ is unbounded.
When the integrator $\alpha$ is not necessarily monotone but of bounded variation then we can use the following definition of integrability (equivalent to others). This is that there exists a real number $I$ such that for any $\epsilon > 0$ there exists $\delta > 0$ such that for any partition $P = (x_0,x_1, \ldots,x_n)$ with mesh $\|P\|< \delta$ and any Riemann-Stieltjes sum $S(P,f,\alpha) = \sum_{j=1}^n f(\xi_j)( \alpha(x_j) - \alpha(x_{j-1}) )$, we have $|S(P,f,\alpha) - I| < \epsilon$. It is proved here that this definition can never be satisfied if $f$ is unbounded.
To prove (a) we must consider a partition $P = (x_0,x_1, \ldots,x_n)$ and
$$\tag{*}V(F,P) = \sum_{j=1}^n \left|F(x_j) - F(x_{j-1}) \right| = \sum_{j=1}^n \left|\int_{x_{j-1}}^{x_j} f \, d\alpha\right|, $$
and show that $\sup_PV(F,P) < \infty$.
When $f$ is bounded the proof is easy. As an alternative proof, note that when $\alpha$ is of bounded variation we have
$$\left|\int_{x_{j-1}}^{x_j} f \, d\alpha\right| \leqslant \int_{x_{j-1}}^{x_j} |f| \, dv_\alpha(x),$$
where $v_\alpha(x) = V_a^x(\alpha)$ is the total variation of $\alpha$ on $[a,x]$.
Thus, for any partition $P$,
$$V(F,P) \leqslant \sum_{j=1}^n \|f\|_\infty \int_{x_{j-1}}^{x_j} \, dv_\alpha(x)=\|f\|_\infty\sum_{j=1}^n V_{x_{j-1}}^{x_j}(\alpha) \leqslant \|f\|_\infty V_a^b(\alpha) < \infty$$
If $f$ is unbounded then the RHS of (*) is not even defined. So to prove that $F$ is of bounded variation we would have to assume that the integrals on the RHS are finite in the sense of improper Riemann-Stieltjes integrals.
Then it gets very messy in that we need to consider if there are a finite number of points where $f$ is unbounded, a countable number of such points , etc. I suspect it could be proved for a finite number of points where $f$ is unbounded.
