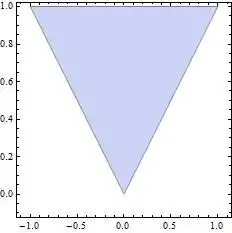
Show that the random variables $X$ and $Y$ are uncorrelated but not independent

Question

Show that the random variables $X$ and $Y$ are uncorrelated but not independent

The given joint density is

$f(x,y)=1\;\; \text{for } \; -y<x<y \; \text{and } 0<y<1$, otherwise $0$

My main concern here is how should we calculate $f_1(x)$

$f_1(x)=\int_y dy = \int_{-x}^{1}dy + \int_{x}^{1}dy = 1+x +1=2\; \; \forall -1 <x<1$

OR Should we do this?

$f_1(x)$=$$ \begin{cases} \int_{-x}^{1}dy = 1+x && -1<x<0 \\ \int_{x}^{1}dy = 1-x & & 0\leq x <1 \\ \end{cases} $$

In the second case, how do I show they are not independent.

I can directly say that the joint distribution does not have a product space but I want to show that $f(x,y)\neq f_1(x)f_2(y)$

Also, for anyone requiring further calculations,

$f_2(y) = \int dx = \int_{-y}^{y}dx = 2y$

$\mu_2= \int y f_2(y)dy = \int_{0}^{1}2y^2 = \frac23$

$\sigma_2 ^2 = \int y^2f_2(y)dy - (\frac23) ^2 = \frac12 - \frac49 = \frac1{18}$

$E(XY)= \int_{y=0}^{y=1}\int_{x=-y}^{x=y} xy f(x,y)dxdy =\int_{y=0}^{y=1}\int_{x=-y}^{x=y} xy dxdy$ which seems to be $0$? I am not sure about this also.

Answer 1

$f_1(x)=1+x$ if $-1<x<0$ and $1-x$ if $0<x<1$. ( In other words $f_1(x)=1-|x|$ for $|x|<1$). As you have observed $f_2(y)=2y$ for $0<y<1$. Now it is basic fact that if the random variables are independent then we must have $f(x,y)=f_1(x)f_2(y)$ (almost everywhere). Since the equation $(1-|x|)(2y)=f(x,y)$ is not true we can conclude that $X$ and $Y$ are not independent.

$EXY=0$ is correct. Also $EX=\int_{-1}^{1}x(1-|x|)dx=0$ so $X$ and $Y$ are uncorrelated.

Answer 2

A slightly different approach:

Joint density of $(X,Y)$ is

\begin{align} f(x,y)&=1_{-y<x<y\,,\,0<y<1} \\&=\underbrace{\frac{1_{-y<x<y}}{2y}}_{f_{X\mid Y=y}(y)}\cdot\underbrace{2y\,1_{0<y<1}}_{f_Y(y)} \end{align}

Since (conditional) distribution of $X$ 'given $Y$' depends on $Y$, clearly $X$ and $Y$ are not independent. In fact, $X$ conditioned on $Y=y$ has a uniform distribution on $(-y,y)$, which gives $E\,[X\mid Y]=0$.

Therefore, by law of total expectation,

\begin{align} E\,[XY]&=E\left[E\left[XY\mid Y\right]\right] \\&=E\left[YE\left[X\mid Y\right]\right] \\&=0 \end{align}

Similarly $E\,[X]=E\left[E\,[X\mid Y]\right]=0$, so that $\operatorname{Cov}(X,Y)=E\,[XY]-E\,[X]E\,[Y]=0$.

---

A more intuitive way to see that two jointly distributed variables $X,Y$ are not independent is to verify that the joint support of $(X,Y)$ cannot be written as a Cartesian product of the marginal supports of $X$ and $Y$. For this, all we need to do is sketch the support of $(X,Y)$ given by $$S=\{(x,y)\in\mathbb R^2: |x|<y<1 \}$$

In fact $(X,Y)$ is uniformly distributed over $S$, which looks like

So support of $X$ is $S_1=(-1,1)$ and that of $Y$ is $S_2=(0,1)$.

But since $S\ne S_1 \times S_2$, the random variables $X$ and $Y$ are not independent.

Related:

• Uncorrelated, Non Independent Random variables
• The mutual density of $X,Y$ in $\{|t|+|s|<1\}$ is constant, are $X,Y$ independent?