Entropy solution to inviscid Burgers with triangular initial data

Question

Find the entropy solution of $$\begin{cases} u_t + \left( \frac{u^2}{2} \right)_x = 0 & \text{ in } \mathbb{R}\times(0,\infty) \\ u = g & \text{ on } \mathbb{R}\times\{0\}, \end{cases}$$ where $$g(x) = \begin{cases} 0&\text{ if } x\leq -1 \\ 1+x&\text{ if } -1\leq x\leq 0 \\ 1-x&\text{ if } 0\leq x\leq 1 \\ 0&\text{ if }x\geq 1. \end{cases}$$

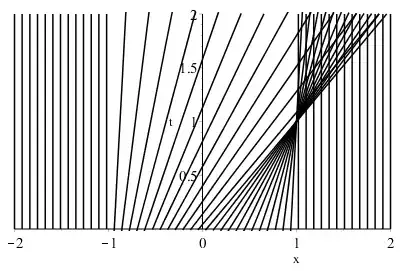
This is what I have so far. To get the characteristics we have $x=g(x_0)t+x_0$ which gives us $$\begin{cases} x_0&\text{ if } x_0<-1 \\ (1+x_0)t+x_0&\text{ if } -1<x_0<0 \\ (1-x_0)t+x_0&\text{ if } 0<x_0<1 \\ x_0&\text{ if } x_0>1 \end{cases}$$ After this step I get a bit confused. I believe the next step is finding the equations for the shocks at the discontinuous points, in this case $(-1,0)$, $(0,0)$, and $(1,0)$. Here is my attempt at calculating the shocks: $$ \frac{dx}{dt} = \frac{0+(1+x)}{2} = \frac{1+x}{2} ~~~~~\Rightarrow~~~~~ \int_x^{-1}\frac{dy}{1+y} = \int_0^t \frac{ds}{2} ~~~~~\Rightarrow~~~~~ \boxed{x=e^{-t/2}-1}$$

$$\frac{dx}{dt} = \frac{(1+x)+(1-x)}{2} = \frac{2}{2} = 1 ~~~~~\Rightarrow~~~~~ \int_0^x dy = \int_0^t ds ~~~~~\Rightarrow~~~~~ \boxed{x=t}$$

$$\frac{dx}{dt} = \frac{(1-x)+0}{2} = \frac{1-x}{2} ~~~~~\Rightarrow~~~~~ \int_1^x \frac{dy}{1-y} = \int_0^t \frac{ds}{2} ~~~~~\Rightarrow~~~~~ \boxed{x=1-e^{-t/2}}$$

Assuming I've done everything right so far, I'm lost after this point. How do I get my entropy solution from this? Also, are there other shocks I need to look at? For example, where my current shocks intersect do new shocks get created?

Any help, guidance, and feedback is greatly appreciated.

Answer 1

Following the steps in this post, the solution $u = g(x-ut)$ obtained with the method of characteristics reads $$ u(x,t) = \left\lbrace \begin{aligned} &0 &&\text{for}\; x < -1\\ &\tfrac{1+x}{1+t} &&\text{for}\; {-1}\leqslant x \leqslant t\\ &\tfrac{1-x}{1-t} &&\text{for}\; t\leqslant x \leqslant 1\\ &0 &&\text{for}\; x > 1 \end{aligned} \right. $$ which is valid for times $0\leqslant t <1$. At the breaking time $t=1$, the base characteristics intersect in the $x$-$t$ plane:

Starting from the breaking time, the entropy solution includes a shock wave, which abscissa $x_s(t)$ satisfies the Rankine-Hugoniot condition. Here, the value on the left of the shock is $\tfrac{1+x_s}{1+t}$, while the value on the right is zero. Thus, the shock trajectory satisfies $$ \frac{\text d x_s}{\text d t} = \frac{1}{2}\left(\frac{1+x_s}{1+t} + 0\right) $$ with $x_s(1)=1$. Therefore, $x_s(t) = \sqrt{2(1+t)} - 1$, and the entropy solution for $t>1$ reads $$ u(x,t) = \left\lbrace \begin{aligned} &0 &&\text{for}\; x < -1\\ &\tfrac{1+x}{1+t} &&\text{for}\; {-1}\leqslant x < x_s(t)\\ &0 &&\text{for}\; x > x_s(t) \end{aligned} \right. $$ The solution is maximal at the left of the shock, and the supremum $u|_{x=x_s^-} = \sqrt{2/(1+t)}$ goes to zero as $t$ goes to infinity.