Book questions on supremum, bounds.

Question

Need help in vetting my answers for the questions 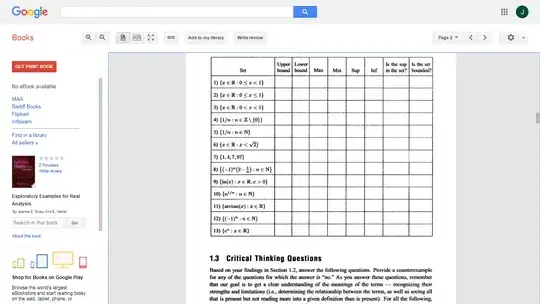in CRM series book by MAA: Exploratory Examples for Real Analysis, By Joanne E. Snow, Kirk E. Weller. I am particularly suspicious about my results in row no. 6, 8, 9, 10, 13.

The book gives the definitions also:

1. A real number $u$ is said to be an upper bound for a set $A$ if $x\le u, \, \forall x\in A$.
   
2. A real number $l$ is said to be an lower bound for a set $A$ if $l\le x, \, \forall x\in A$.
   
3. A set is bounded if it possesses both an upper bound & lower bound.
   
4. A real number $s$ is the supremum, or least upper bound, of a set $A$ if $s$ is an upper bound of $A$ and $s \le u$ for any other upper bound $u$ of $A$. It is denoted by $\sup(A)$.
   
5. A real number $t$ is the infimum, or greatest lower bound, of a set $A$ if $t$ is a lower bound of $A$ and $t \ge l$ for any other lower bound $l$ of $A$. It is denoted by $\inf(A)$.
   
6. A real number $m$ is the maximum of a set $A$ if $m \in A$ and $x \le m, \,\, \forall x \in A$.
   
7. A real number $n$ is the minimum of a set $A$ if $n \in A$ and $x \ge n, \,\, \forall x \in A$.

Notation : $R= $ real numbers, $Z=$ integers, $N=$ natural numbers.

• If a set fails to have any property, write DNE.
  

• For the last two columns, write Yes/No

Due to presentation reasons, am splitting response by showing answers for last four columns later.

$$\begin{array}{c|c|c|c|c|} Set & \text{U.B.} & \text{L.B} & \text{Max} & \text{Min} \\ \hline \text 1)\,\ \{x\in \mathbb{R}: 0\le x \lt 1 \} & 1 & 0 & DNE& 0\\ \hline \text 2)\,\ \{x\in \mathbb{R}: 0\le x \le 1 \} & 1 & 0 & 1 & 0 \\ \hline \text 3)\,\ \{x\in \mathbb{R}: 0\lt x \lt 1 \} & 1& 0&DNE & DNE\\ \hline \text 4)\,\ \{\frac 1n: n \in \mathbb{Z}-\{0\}\} & 1 & -1 & 1 & -1\\ \hline \text 5)\,\ \{\frac 1n: n \in \mathbb{N}\} & 1& 0&1 &DNE \\ \hline \text 6)\,\ \{x\in \mathbb{R}: x \lt \sqrt{2} \} & (\sqrt{2},\infty) & DNE& DNE & DNE \\ \hline \text 7)\,\ \{1,4,7,97\}&97 & 1& 97&1 \\ \hline \text 8)\,\ \{(-1)^n(2-\frac 1n: n\in \mathbb{N} \} &DNE & ?&DNE & ? \\ \hline \text 9)\,\ \{\ln{x}: x\in \mathbb{R}, x \gt 0 \} & DNE\,(\infty)& DNE\,(-\infty)& DNE& DNE\\ \hline \text 10)\,\ \{n^\frac 1n: n \in \mathbb{N} \} & --& 0& --& 0 \\ \hline \text 11)\,\ \{\arctan(x) : x \in \mathbb{R} \} & k.\frac{\pi}2, k\in \mathbb{R{+}} & -k.\frac{\pi}2& \frac{\pi}2& -\frac{\pi}2 \\ \hline \text 12)\,\ \{(-1)^n : n\in \mathbb{N} \} & 1& DNE\,(=-1)& 1 &DNE\,(=-1)\\ \hline \text 13)\,\ \{e^x: x \in \mathbb{R} \}& DNE\,(\infty)& 0& DNE\,(\infty)& 0\\ \hline \end{array}$$

$$\begin{array}{c|c|c|c|c|} Set& \text{Sup}& \text{Inf} & \text{Is Sup. in set?}& \text{Is set bounded?}\\ \hline \text 1)\,\ \{x\in \mathbb{R}: 0\le x \lt 1 \} &1& 0& No & Yes\\ \hline \text 2)\,\ \{x\in \mathbb{R}: 0\le x \le 1 \} & 1 &0 & Yes& Yes \\ \hline \text 3)\,\ \{x\in \mathbb{R}: 0\lt x \lt 1 \} & 1&0&No & Yes\\ \hline \text 4)\,\ \{\frac 1n: n \in \mathbb{Z}-\{0\}\} &1 &-1 & Yes&Yes \\ \hline \text 5)\,\ \{\frac 1n: n \in \mathbb{N}\} & 1& 0& Yes& Yes \\ \hline \text 6)\,\ \{x\in \mathbb{R}: x \lt \sqrt{2} \} & \sqrt{2} & DNE& No &No \\ \hline \text 7)\,\ \{1,4,7,97\} &97 & 1& Yes& Yes \\ \hline \text 8)\,\ \{(-1)^n(2-\frac 1n: n\in \mathbb{N} \} &DNE &? & No & No\\ \hline \text 9)\,\ \{\ln{x}: x\in \mathbb{R}, x \gt 0 \} & DNE\,(\infty)& DNE\,(-\infty)& No & No\\ \hline \text 10)\,\ \{n^\frac 1n: n \in \mathbb{N} \} & --& 0& --& No \\ \hline \text 11)\,\ \{\arctan(x) : x \in \mathbb{R} \} & \frac{\pi}2& -\frac{\pi}2& Yes& Yes \\ \hline \text 12)\,\ \{(-1)^n : n\in \mathbb{N} \} &1 &DNE\,(=-1)& Yes& No \\ \hline \text 13)\,\ \{e^x: x \in \mathbb{R} \} & DNE\,(\infty)& 0& No& No\\ \hline \end{array}$$

Edit:
My explanations are stated below for filling up the rows:

1. $\{x\in \mathbb{R}: 0\le x \lt 1 \} $:
   Upper bound is in the interval $[1,\infty) \in \mathbb{R}$, but written the first value only.
   Lower bound is in interval $(-\infty,0] \in \mathbb{R}$.
   Max. does not belong to the set as the supremum is not in the set. So, DNE is stated.
   Min. is $0$, as it belongs to the closed lower bound.
   Supremum is the least upper bound, & is $1$.
   Infimum is the greatest lower bound, & is $0$ and belongs to the set.
   No, supremum is not in the set.
   Set is bounded.

2. $\{x\in \mathbb{R}: 0\le x \le 1 \} $:
   Upper bound is in the interval $[1,\infty) \in \mathbb{R}$, but written the first value only.
   Lower bound is in interval $(-\infty,0] \in \mathbb{R}$.
   Max. does belong to the set as the upper bound is closed.
   Min. is $0$, as it belongs to the closed lower bound.
   Supremum is the least upper bound, & is $1$.
   Infimum is the greatest lower bound, & is $0$ and belongs to the set.
   Yes, supremum is in the set.
   Set is bounded both from above & below, so bounded.

3. $\{x\in \mathbb{R}: 0\lt x \lt 1 \} $:
   Upper bound is in the interval $[1,\infty) \in \mathbb{R}$, but written the first value only.
   Lower bound is in interval $(-\infty,0] \in \mathbb{R}$.
   Max. does not belong to the set as the supremum is not in the set. So, DNE is stated.
   Min. does not belong to the set as the lower bound is open. So, DNE is stated.
   Supremum is the least upper bound, & is $1$.
   Infimum is the greatest lower bound, & is $0$ and does not belong to the set.
   No, supremum is not in the set.
   Set is bounded.

4. $\{\frac 1n: n \in \mathbb{Z}-\{0\}\}$
   Domain of values is in the set of integers, sans $0$. The max. value of range is at $n=1$, & the min. value of range is at $-1$.
   Upper bound is having only one point $1$.
   Lower bound is having only one point $-1$.
   Max. belongs to the set as $1 \in \mathbb{Z}-\{0\}$
   Min. belongs to the set as $-1 \in \mathbb{Z}-\{0\}$
   Supremum is the least upper bound, & is $1$.
   Infimum is the greatest lower bound, & is $-1$ and belongs to the set.
   Yes, supremum is in the set.
   Set is bounded from above & below, so bounded.

5. $\{\frac 1n: n \in \mathbb{N}\}$
   Domain of values is in the set of naturals. The max. value of range is at $n=1$, & the min. value of range is at $0$, which occurs at $x = \infty$. So, lower bound is $0$, but the range as well as domain point is not in given domain.
   Upper bound is having only one point $1$.
   Lower bound $=0, \not \in \mathbb{N}$ .
   Max. belongs to the set as $1 \in \mathbb{N}$
   Min. does not exist as there is no lower bound
   Supremum is the least upper bound, & is same as the upper bound $=1$.
   Infimum $= 0$.
   Yes, supremum is in the set.
   Set is bounded from below, even though not the lower bound is not in domain.

6. $\{x\in \mathbb{R}: x \lt \sqrt{2} \}$
   Domain of values is in the set of reals. The max. value of range is at $x=\sqrt{2}$, but that value is unattainable. Min. value of range is at $-\infty$. So, lower bound is undefined as that domain point is unreachable.
   Upper bound is in interval $(\sqrt{2}, \infty)$, but confusion over where to start the upper bound starts as $\sqrt{2}$ is an irrational, so non-terminating & non-recurring.
   No Lower bound, so DNE.
   Max. - DNE, as supremum not in set (range).
   Min. - DNE.
   Supremum is the least upper bound. but confusion over where to start the upper bound.
   Infimum is the greatest lower bound, but as lower bound doesn't exist, so it also DNE.
   Confusion exists over supremum is not in set.
   Set is unbounded from below, so un-bounded.

7. $\{1,4,7,97\}$ : skipped

8. $\{(-1)^n(2-\frac 1n: n\in \mathbb{N} \}$:
   Domain of values is in the set of naturals. The max. value of range is at $n=\infty$, but that value is unattainable. Min. value of range is at $n=1$. So, lower bound is undefined as that range point is unreachable in naturals.
   Upper bound has its sole point at $n= \infty$, so DNE.
   Lower bound has sole point at $n=1$, but then the range point is not in naturals. Hence, confusion (?).
   Max. is DNE.
   Min. cannot state, confusion (?).
   Supremum - DNE.
   Infimum - confusion (?).
   Supremum does not exist.
   Set is Unbounded.

9. $\{\ln{x}: x\in \mathbb{R}, x \gt 0 \}$:
   Domain of values is in the set of reals. The max. value of range is at $x=\infty$ , also that value is unattainable. Min. value of range is $x=-\infty$ at values of $x$ near ordinate axis.
   So, both upper & lower bound are undefined. Upper bound is DNE due to both the domain point being unattainable, & the value of range being unattainable too.
   Upper bound at $x= \infty, = \infty$, hence - DNE.
   Lower bound has value at $\lim_{x \to 0^+}$ of $-\infty$, i.e. $\lim_{x \to 0^+} \ln x = -\infty$. Hence - DNE.
   Max. - DNE.
   Min. - DNE.
   Supremum - DNE.
   Infimum - DNE.
   Supremum does not exist.
   Set is Unbounded.

10. $\{n^\frac 1n: n \in \mathbb{N} \}$:
    Domain of values is in the set of naturals.
    I am unable to find minimum, maximum (in range), and list a few values below:

$$\begin{array}{c|c|} & \text{$n\in \mathbb{N}$}& \text{$n^{\frac1n}$}\\ \hline a & 1& 1\\ \hline b & 2& \sqrt{2}\\ \hline c & 3& 3^{\frac13}\\ \hline d & 4& 4^{\frac14}\\ \hline \end{array}$$

The max. /min. value in range of function is unknown by me, hence it needs finding derivative (both first & second).
The eqn. would be :

$y = n^\frac 1n: n \in \mathbb{N}$, with steps to solve being in-complete:
$ \implies \ln y = \frac 1n \ln n \implies \frac 1y y' = \frac 1{n^2}(1-\ln n )$

$y' = n^\frac 1n\frac 1{n^2}(1-\ln n )$

Need to double differentiate the above, but don't know how to pursue further.

Hence, entries for Upper bound, Max., supremum are marked blank.
The lower bound (is $0$) at $n = \infty$, due to $\infty^\frac{1}{\infty}$. However, the domain value of $n =\infty$ is unattainable, so DNE.

11. $\{\arctan(x) : x \in \mathbb{R} \}$:
    Domain of values is in the set of reals. Have taken radian value. Although, upper & lower bounds can have set of integer multiples ($k$). But, the values of max., infimum, min., supremum have to be unique; so taken their values only in $[0,2\pi]$ range.

12. $\{(-1)^n : n\in \mathbb{N} \}$:
    Domain of values is in the set of naturals. The range comprises of two values : $\{-1,1\}$ & the max. value of range is $1$ for even $n$, while the min. value is $-1$ for odd $n$. The value of $-1\not \in \mathbb{N}$, so the corresponding values (Min., infimum, Lower bound) are DNE.

13. $\{e^x: x \in \mathbb{R} \}$:
    Domain of values is in the set of reals. The max. value of range is $\infty$ at $x=\infty$, but that value is unattainable. Min. value of range is $0$ at values of $x=-\infty$. So, both upper & lower bound are undefined, but for different reasons.
    Lower bound has at $-\infty$ an open bound of $0$, hence - DNE.
    Lower bound is $0$ at $x \to -\infty$.
    Upper bound is DNE due to both : domain point being unattainable, & value of the range.
    Upper bound at $x \to \infty = \infty$, hence - DNE.
    
    Max. - DNE.
    Min. - DNE, as infimum value is not 'achieved' at an attainable real in domain. 0
    Supremum - DNE.
    Infimum - $0$.
    Supremum does not exist.
    Set is Unbounded.

Answer 1

• If the supremum is in the set, then the maximum exists. Use this principle to check your solution again.

• For part $5$, for which $n$ does $\frac1n = 0$. What should this tell you about whether minimum exists?

• For part $6$, notice that $\sqrt{2} > 1.42$, notice that $\sqrt2 \ne 1.42$.

• For part $8$, what do you mean by $-1$ does not exists? Also, for the same question, how do you attain $2$? If the supremum exists and the infimum exists, the set is bounded.

• For part $10$, try $n=2$ and we can show that $\sqrt2$ is in the set and $\sqrt2 > 1$. Again, what do you mean by $DNE=0$.

• For part $11$, if the maximum exists, it is unique.

• For part $12$, again, what do you mean by $-1$ DNE? If supremum and infimum exists, it is bounded.

• For part $13$, how do you solve for $e^x=0$?

Edit:

1. You need to work on writing things more carefully. For example, "Max. does not belong to the set as the upper bound is open." hmmm... this sentence makes no sense to me. What do you mean by the upper bound? why does it justify that the maximum does not belong to the set, in the first place, the maximum should exists for you to talk about whether it belong to a set. Perhaps you want to talk about the supremum does not belong to the set. I can guess what you mean but learn to slow down and write things clearly.

2. Do not write min is $0$ if the min doesn't exists. You should learn to prove that the infimum is $0$. You should prove that $0$ is a lower bound for your set.

3. The set doesn't have a maximum (prove it) if the supremum is unattainable. There is nothing wrong with an irrational number being an upperbound. Verify things from the definition.

4. If you can't understand the set, explicitly write down a few terms. Every entry in the row is not correct.

5. Correction: The domain is the set of positive real number. Avoid using term like maximum and minimum unless they exists. Can't follow your reasoning. $\lim_{x \to 0^+} \ln x = -\infty$ and it can get arbitrarily negative.

10/ 11. Too long.

12. The set $\{ (-1)^n : n \in \mathbb{N} \}= \{-1,1\}$. $-1$ is the smallest value of the set. $-1$ is in the set.

13. $e^x>0$. Again, what do you mean by maximum and minimum value if it doesn't exist. The part about lower bound and infimum are not correct.