0

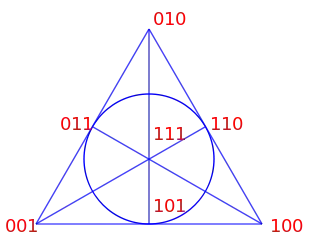
Problem: Show that any two points in Fano plane are not contained in exactly two lines of the plane and their sum is contained in those two lines in which $p$ and $q$ are not contained.

My attempt: For the proof we will use Homogeneous coordinates, that is triples with elements of the field $\mathbb{F}_2$. We will construct Fano plane in such a way that for any two points $p$ and $q$ the third point on the line has the label formed by adding the labels of $p$ and $q$ modulo 2.

enter image description here

Take any two arbitrary points $p$ and $q$, which are not equal. Then $p,q \in \mathbb{F}_2^{3*}$. Then $p,q$ are both contained in a line where the third point is the sum of $p$ and $q$. Hence on each line of the Fano plane there are two linearly independent points and third one is formed in a way that it is the sum of the linearly independent points.

I am stuck right now could anyone please explain or give hints? Why each point is contained in exactly three lines?

Jyrki Lahtonen
  • 140,891

3 Answers3

2

I do not quite understand your Problem (the sum of two points in contained in both of what?).

However, as to your last question, let $a$ be any point. Then for each point $b \ne a$, $a$ is contained in the line $a, b, a+b$. Since two distinct points determine a line, any two distinct lines of this form have only $a$ in common. Thus each line contribute $2$ points besides $a$. Since $7 = 1 + 2 \cdot 3$, there are exactly three lines containing $a$.

Andreas Caranti
  • 70,862
  • I made an edit. But the problem is the following: –  Apr 21 '19 at 17:32
  • We observe from the fano plane that if we take any two points, say $p$ and $q$ then they are not contained in exactly two lines. And the sum of this two points lie on exactly those two lines on which $p$ and $q$ do not lie –  Apr 21 '19 at 17:33
  • Why does the point a contained in a line b? Could you please explain using Homogeneous labeling? Since otherwise I am confused –  Apr 21 '19 at 17:48
2

Andreas Caranti already explained why each point belongs to exactly three lines. The other question can be settled as follows.

Let $p$ and $q$ be the two points in question. The third point on the line determined by $p$ and $q$ is thus $p+q$. We know that $p+q$ is on exactly three lines. Call them $L_1$, $L_2$ and $L_3$. Without loss of generality $L_1=\{p,q,p+q\}$.

The point $p$ cannot belong to either $L_2$ or $L_3$ for then there would be two lines containing both $p$ and $p+q$. Similarly we see that $q$ cannot be on either $L_2$ or $L_3$ either.

Recall that there are $7$ lines. The point $p$ lies on exactly three of them - two others in addition to $L_1$. By the above observation these two lines are previously unnamed, so we choose to call them $L_4$ and $L_5$. Observe that neither of them can contain $q$. Therefore the lines containing $q$ are $L_1$ and the two yet unnamed lines $L_6$ and $L_7$.

We have covered all the seven lines, and our census gives the conclusion: $L_2$ and $L_3$ are the only lines not containing either $p$ or $q$. As required, those were also the two lines passing thru $p+q$ (excluding $L_1$).

Jyrki Lahtonen
  • 140,891
1

I'll begin by saying that I have very little knowledge about this area of math. However, regarding the last part of your problem.

Either I'm misunderstanding the question, or it is wrong. Take any two points $p$ and $q$, then their sum is by definition the third point on the line which both $p$ and $q$ lie on. Also, as shown by Andreas, any point lies in three distinct lines, so the sum of $p$ and $q$ can't lie on 'those two lines in which p and q are not contained.'

Maybe someone with more knowledge can shed some light on this.

Auclair
  • 1,487