Obtaining the Parameterization of a Space-Filling Curve

Question

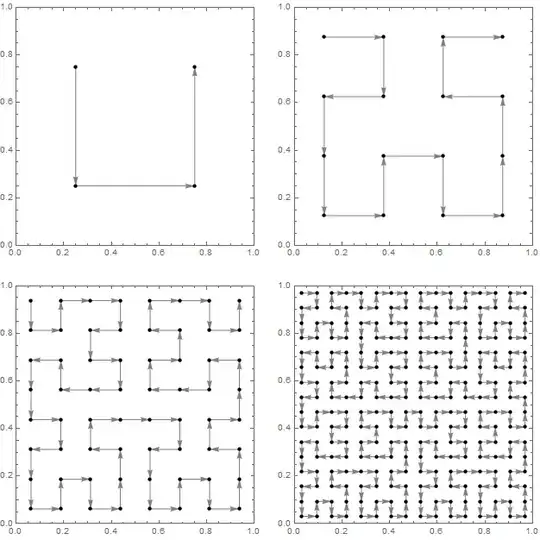
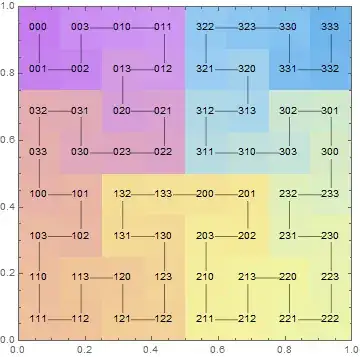
So, I am working with a grid that has $N_x$, $N_y$ and $N_z$ voxels along the $x$, $y$ and $z$ axis respectively. There is this bijection that I apply in order to use the grid as one large vector and it is as such:

$$ \tag{1} \label{eq:param} l(i,j,k)=i⋅(N_x)^2+j⋅(N_y)^1+k⋅(N_z)^0 $$

where $i,j,k$ are the indices of a voxel in the grid. It occurred to me that this is a very arbitrary way of having a grid turned into a vector, of converting 3D to 1D and I started looking into it a little bit more. I came across the concept of a space-filling curve and it seemed to me like those curves were better behaved and had interesting properties.

I wanted to work with them, it turns out that in order to do that I need a way to compute the values $l(i,j,k)$ for these curves. So my question is:

Is there a way to obtain a parameterization such as the one in Equation \ref{eq:param} for a space-filling curve?

P.S. If there is no general method, it is enough to discuss one particular example of a space-filling curve where that is possible.

P.P.S. In case there are no examples with a neat closed-form expression like Equation \ref{eq:param}, it is okay if there is a computational procedure to compute an $l(i,j,k)$, given the indices $i,j$ and $k$.

Answer 1

Some space-filling curves, such as Peano curve and Hilbert curve, can be regarded as certain generalization of $d$-ary expansion. This is because $d$-ary expansion on the unit interval $[0, 1]$ can be thought as parametrizing $[0, 1]$ by the infinite rooted $d$-ary tree $T_d = \{0, \cdots, d-1\}^{\mathbb{N}}$, and likewise, the aforementioned curves can also be parametrized by $T_d$ for certain choices of $d$.

For instance, let $\gamma : [0, 1] \to [0, 1]^2$ be the Hilbert curve as in the construction illustrated in here. Its first four steps are demonstrated below:

Now we recursively define $S_a$'s as follows:

• Set $S_{\varnothing} = [0, 1]^2$.

• Let $n \geq 1$ and $a = (a_1, \cdots, a_{n-1})$, where the empty list is denoted by $\varnothing$. If $S_a$ is defined, then divide $S_a$ into $4$ sub-squares of equal sizes. In order to label them, define $e_1, \cdots, e_{n-1}$ by

  $$ e_i = \begin{cases} (1, 0), & a_i = 0; \\ (0, 0), & a_i = 1 \text{ or } 2; \\ (1, 1), & a_i = 3 \end{cases} \qquad \text{and} \qquad e = \sum_{i=1}^{n-1} e_i \pmod{2}. $$

  Although the meaning of $e$ is not clear at this moment, we remark that $e$ determines the shape of the curve on $S_a$. Then label the sub-squares by the following rules:

  

Then we have:

Proposition. For any $x \in [0, 1]^2$, let $a_1, a_2, \cdots \in \{0,1,2,3\}$ be such that $x \in S_{a_1,\cdots,a_n}$ for all $n \geq 1$. If $t = 0.a_1 a_2 \cdots _{(4)}$ denotes the $4$-ary expansion with digits $a_1, a_2, \cdots$, then $\gamma(t) = x$.

For instance, the following picture shows the regions corresponding to different values of the first 3 digits $(a_1, a_2, a_3)$:

This plot also suggests why we adopt the above weird-looking labeling rule. It simply labels sub-squares according to their order of appearance along the Hilbert curve.