5

How would you go around proving that there exists a heteroclinic orbit between two equilibria ( in the problem I'm trying to solve, one is a stable node(say n) and the other is a saddle (say s))?

I started by finding the stable manifold of the stable node and the unstable manifold of the saddle point.

Next, I want to show that their intersection is not empty and so there must be a trajectory that starts at s and end at n. And therefore, a heteroclinic orbit. But the problem is that the stable manifold only "covers" a neighborhood of n. Same for the unstable manifold.

So how do we figure out the neighborhoods I guess? Or is there a better way to do this than using the stable and unstable manifolds?

Edit: This is the system of ODEs I'm dealing with. $$U' = V\\ V' = -\frac{c}{D}V -\frac{\mu}{D} U (1-U)\\$$ All of the parameters are positive. and $c>\sqrt{4\mu D}$. So we have two equilibria: A stable node: (U,V) = (0,0). And a saddle point: (U,V) = (1,0).

Thanks

Rasha Nasri
  • 51
  • 2

1 Answers1

1

Let's rewrite the system of ODEs as a second order ODE: $$ U''=V'=-\frac{c}{D}V-\frac{\mu}{D}U(1-U)=-\frac{c}{D}U'-\frac{\mu}{D}U(1-U). \tag{1} $$ It follows from $(1)$ that $$ \frac{d}{dt}\left[\frac{1}{2}(U')^2+\frac{\mu}{D}\left(\frac{1}{2}U^2-\frac{1}{3}U^3\right)\right]=-\frac{c}{D}(U')^2\leq 0. \tag{2} $$ If we interpret $(1)$ as the Newtonian equation of motion of a particle subject to the force $F=-\frac{c}{D}U'-\frac{\mu}{D}U(1-U)$, then Eq. $(2)$ expresses the dissipation of mechanical energy $E=\frac{1}{2}(U')^2+\frac{\mu}{D}\left(\frac{1}{2}U^2-\frac{1}{3}U^3\right)$ due to the viscous frictional force $-\frac{c}{D}U'$.

Let's now show that there is a trajectory that satisfies $\lim_{t\to-\infty}(U(t),U'(t))=(1,0)$ and $\lim_{t\to+\infty}(U(t),U'(t))=(0,0)$. When $|U(t)-1|\ll 1$, we can linearize $(1)$ as $$ U''+\frac{c}{D}U'-\frac{\mu}{D}U\approx -\frac{\mu}{D}. \tag{3} $$ Equation $(3)$ has a solution that satisfies $\lim_{t\to-\infty}(U(t),U'(t))=(1,0)$, given by $$ U(t)=1+Ae^{\lambda t},\quad\text{where}\quad \lambda:=\frac{-c+\sqrt{c^2+4\mu D}}{2D}>0. \tag{4} $$ If $A<0$, the particle initially moves to the left. Because of $(2)$, $E(t)<E(-\infty)=\frac{\mu}{6D}$ for any finite $t$, so the particle gets trapped in the potential well $\mathcal{V}(U):=\frac{\mu}{D}\left(\frac{1}{2}U^2-\frac{1}{3}U^3\right)$ to the left of $U=1$ (see figure below).

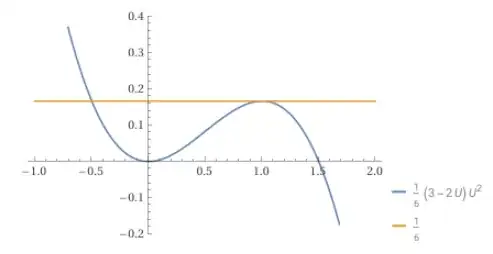
Potential well

Although the solution $(4)$ is valid only for times $t$ such that $|Ae^{\lambda t}|\ll 1$, we can base the rest of our argument on the inequality $(2)$, which is valid for all $t$. Since $E(t)$ is a non-increasing function of $t$ and is bounded below (once the particle is trapped in the potential well), $E(t)$ tends to a finite limit as $t\to\infty$. Since this limit is a constant, it follows from $(2)$ that $\lim_{t\to\infty}U'(t)=0$, hence $\lim_{t\to\infty}U''(t)=0$ too. Equation $(1)$ then implies $\lim_{t\to\infty}U(t)[1-U(t)]=0$; since $U(t)<1$ for $t>-\infty$, it follows that $\lim_{t\to\infty}U(t)=0$. This completes the proof of existence of an heteroclinic orbit between the equilibrium points $(1,0)$ and $(0,0)$.

Gonçalo
  • 15,869