I am trying to find good ways to tackle sums of the form $$\sum_{k=1}^{N}k^j\varphi(k)$$ $j$ can be anything but I am largely concerned about cases $0$, $1$, and $2$.
$\varphi(k)$ is the Euler totient function.
Can this be done without needing to calculate $k^j\varphi(k)$ manually for every single step of $k$? Is there any optimization opportunity? Any identities that apply here that might help?
(This answer has been rewritten as a detour of Dirichlet convolution blog post by adamant)
Many sums of arithmetic functions like $\Phi(n) = \sum_{k\le n} \varphi(k)$ can be solved in sublinear time using the Dirichlet hyperbola method. Recall the Dirichlet convolution for arithmetic functions $f, g$: $$(f * g)(n) = \sum_{d|n} f(d) g \left(\frac n d\right) = \sum_{ij = n} f(i) g(j) $$ $\newcommand{\floor}[1]{\left\lfloor #1 \right\rfloor}$ Let $F$ and $G$ be the summatory functions of $f$ and $g$, i.e. $F(x) = \sum_{i \le x} f(i)$ and $G(x) = \sum_{j \le x} g(j)$. These summatory functions have their domain extended to reals, as the indices are over positive integers $\le x$. Another way of putting it using only integer bounds is $F(x) := F(\floor{x})$. This will be useful for counting later.
We want to find the sum of the convolution, $\sum_{t \le n} (f * g)(t)$. Using the hyperbola method, we can compute this in terms of $f, g$ and their summation functions $F, G$.
From the first equation, the sum of the Dirichlet convolution is $$ \sum_{t \le n} (f * g)(t) = \sum_{t \le n} \sum_{d | t} f(d) g \left( \frac t d \right) = \sum_{ij \le n} f(i) g(j) $$
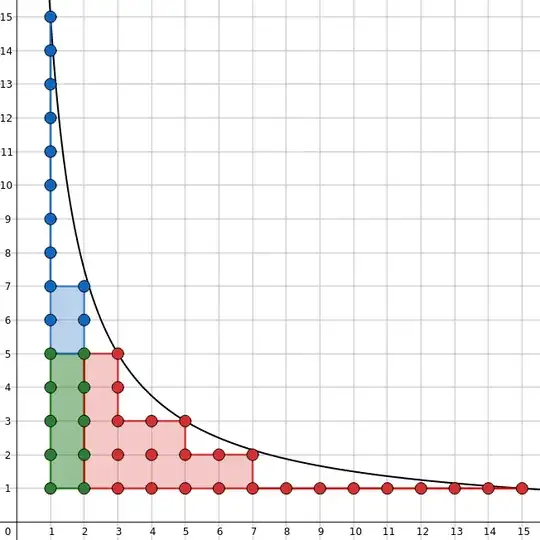
Lattice points under $ij = 15$. Credit: adamant.
In our case, we start with the $\operatorname{Id} = \varphi * \mathbf 1$, another way of writing the identity $$n = \sum_{d|n} \varphi(d) $$
We want to find $\Phi$, the sum of $\varphi$, and the sums of the others are easy: $\sum_{k\le n} \operatorname{Id}(k) = T(n)$, the triangular numbers, and $\sum_{k \le n} \mathbf 1 (k) = n = \operatorname{Id}(n)$. Thus in our case $f = \mathbf 1, F = \operatorname{Id}, g = \varphi, G = \Phi, f * g = \operatorname{Id}, \sum (f * g) = T$.
The key is that summation over $ij \le n$ is the hyperbola shape. The usual hyperbola method makes use of the fact that one of $i$ or $j$ is less than $\sqrt n$ (see below), but for this particular problem we can simplify the sum since $f$ is so simple. Observe for each $i$, the values of $j$ under the hyperbola are from $1$ up to $n/i$. That is, $$\sum_{ij \le n} f(i) g(j) = \sum_{i \le n} f(i) \sum_{j \le n/i} g(j) = \sum_{i \le n} f(i) G \left( \frac n i \right) $$
This identity is the starting point of the recursive algorithms: $$ T(n) = \sum_{i=1}^n \Phi \left(\frac n i\right) $$
By a generalization to the Möbius inversion formula,
$$\Phi(n) = \sum_{i=1}^n \mu(i) \ T \left( \frac n i \right)$$
Since $\mu(i)$ for range $[1,n]$ can be computed in linear time using a linear sieve, this gives a linear time and space algorithm. However, we can already use a small modification to the Sieve of Eratosthenes to compute $\varphi$ for the whole range in $O(n \log \log n)$ time, so we didn't make that much progress here.
Instead, the hyperbola shape suggests a sub-linear algorithm. Rearrange to solve for $\Phi(n)$: $$\Phi(n) = T(n) - \sum_{i=2}^n \Phi \left(\frac n i \right)$$
The observation is that for large $i$ (consider $i \ge \sqrt n$), $\floor{n/i}$ is constant for many values. Let this cutoff point be $c = \floor{\sqrt n}$. We can calculate precisely how many times each possible value occurs.
$$ \floor{\frac n i} = \begin{cases} 1 & \text{if } n/2 < i \le n \\ 2 & \text{if } n/3 < i \le n/2 \\ \vdots \\ c-1 & \text{if } n/c < i \le n/(c-1) \\ \end{cases} $$
We can split the sum into two cases:
This gives us our final recursive formula:
$$\Phi(n) = T(n) - \sum_{2 \le i \le n/c} \Phi \left(\frac n i \right) - \sum_{j \le c-1}\left( \floor{\frac n j} - \floor{ \frac n {j+1} } \right) \Phi(j) $$
What is the time complexity for the top level call $\Phi(N)$, assuming we memoize results? Since we chose $c \approx \sqrt N$, both summations each do about $\sqrt N$ recursive calls.
For $\Phi(N/i)$ term, all recursive calls use only values needed for the top-level $\Phi(N)$, as $\floor{\floor{N/i}/i'} = \floor{N/ii'}$. Assume for simplicity we can pre-compute all $\Phi(j)$ for $j \le \sqrt N$ in linear time, and retrieve values in $O(1)$. The total computation is bounded by something roughly like $\sum_{j=1}^{\sqrt N} O(1) + \sum_{i=2}^\sqrt N O(\sqrt{N/i}) = O(N^{3/4})$. See this answer by Erick Wong for more details.
The Codeforces post by adamant has a more detailed explanation and details on using pre-computed prefix sums for a better time complexity. The idea for this method is that you can compute $\Phi$ and prefix sums up to $c = n^{2/3}$ in linear time with a linear sieve, so $O(n^{2/3})$. Then we only need $\Phi(n/i)$ for $i$ up to $n/c = \sqrt[3]{n}$. The sum is computed in $\sum_{i=1}^{\sqrt[3]{n}} O(\sqrt{n/m}) = O(n^{2/3})$, which is balanced with the pre-computational cost. This is theoretically better than $O(n^{3/4})$, but at this point constant factors matter. In my experience, pre-computing up to $c = \sqrt n$ is the fastest.
If we apply the simplified method to general functions $f, g$, for each $j$ there are $\sum_{n/(j+1) < i \le n/j} f(i)$ values, so the formula ends up as $$ \sum_{i\le n} f(i) G \left(\frac n i \right) = \sum_{i \le n/c} f(i) G \left( \frac n i \right) + \sum_{j\le c-1} \left( F \Bigl( \frac n j \Bigr) - F \Bigl( \frac n {j+1} \Bigr) \right) G(j) $$
The general Dirichlet hyperbola method considers for a cutoff point of $\sqrt n$ that at least one of $i$ or $j$ is $\le \sqrt n$. So we sum up points $i \le \sqrt n$ plus points $j \le \sqrt n$ minus overlap. This is essentially the same as the last formula, when we were more careful with counting to prevent overlap. This version highlights the symmetry much better.
$$ \sum_{ij \le n} f(i) g(j) = \color{blue} {\sum_{i \le \sqrt n} f(i) G \Bigl( \frac n i \Bigr) } + \color{red}{ \sum_{j \le \sqrt n} g(j) F \Bigl( \frac n j \Bigr) } - \color{green} { F(\sqrt n) G(\sqrt n) } $$
Again we can choose a different cutoff covering all points using $i \le n/c$ and $j \le c$, if the computation times for $f, g, F, G$ are very different.
$$ \sum_{ij \le n} f(i) g(j) = \color{blue} {\sum_{i \le n/c} f(i) G \Bigl( \frac n i \Bigr) } + \color{red}{ \sum_{j \le c} g(j) F \Bigl( \frac n j \Bigr) } - \color{green} { F(n/c) G(c) } $$
For the case $j=0$, you can define some auxiliary summations to formulate an algorithm that runs in $O(n^{3/4})$ time:
$$F(N) = \lvert \{ a,b : 0 < a < b \le N \} \rvert$$
$$R(N) = \lvert \{ a,b : 0 < a < b \le N, \gcd(a,b) = 1 \} \rvert$$
You can see that we are looking for $R(N) + 1$. Also, $F(N)$ is $\dfrac{N(N-1)}{2}$.
Now observe something nice:
R$\left( \Big\lfloor\dfrac{N}{m}\Big\rfloor \right)$ = $\lvert \{ a,b : 0 < a < b \le N, \gcd(a,b) = m \} \rvert$
Why? This is because you can multiply every coprime pair of $(a,b)$ by $m$.
This fact lets you write $F$ in terms of $R$:
F(N) = $\displaystyle\sum_{m=1}^N{ R\left(\Big\lfloor\dfrac{N}{m}\Big\rfloor\right) } $
Since we are looking for $R(N)$, we solve for the first term of the right summation.
$R(N) = F(N) - \displaystyle\sum_{m=2}^N{ R\left(\Big\lfloor\dfrac{N}{m}\Big\rfloor\right) } $
Note this interesting property of the floor function here: $\Big\lfloor\dfrac{N}{m}\Big\rfloor$ will stay constant for a range of $m$. This lets us calculate the summation in chunks. example:
$\Big\lfloor\dfrac{1000}{m}\Big\rfloor$ is constant for $m$ in the range of [501,1000].
Here's a program I wrote in C++ that caches R to trade O(log n) memory for a large speedup
Andy already described pretty well how to calculate $R_0$ in sublinear time. It is important to memoize results of already calculated $R_j$ in order to avoid duplicate computations. Here is a general formula for any $j\geq0$:
$$R_j(n) = \sum\limits_{k=1}^n k^j \varphi(k) $$
$$S_j(n) = \sum\limits_{k=1}^n k^j$$ $$R_j(n) = S_{j+1}(n) - \sum\limits_{k=2}^n k^j R_j\left ( \left \lfloor \frac{n}{k} \right \rfloor \right )$$
Notice that $S_j$ is just a polynomial of degree $j+1$: $$S_1(n) = \frac{1}{2}n(n+1)$$ $$S_2(n) = \frac{1}{6}n(n+1)(2n+1)$$ $$S_3(n) = \frac{1}{4}n^2(n+1)^2$$
Note that the inner sum can be calculated in $O(\sqrt{n})$ steps (without taking into account calculation of values of $R_j$ which have to be calculated anyway) if we take $q=\lfloor \sqrt{n}\rfloor $:
$$\sum\limits_{k=2}^n k^j R_j\left ( \left \lfloor \frac{n}{k} \right \rfloor \right )$$ $$= \sum\limits_{k=2}^{\lfloor n/q \rfloor} k^j R_j\left ( \left \lfloor \frac{n}{k} \right \rfloor \right ) + \sum\limits_{m=1}^{q-1} \sum\limits_{k=\lfloor \frac{n}{m+1} \rfloor + 1}^{\lfloor \frac{n}{m} \rfloor} k^j R_j(m)$$ $$= \sum\limits_{k=2}^{\lfloor n/q \rfloor} (S_j(k) - S_j(k-1)) R_j\left ( \left \lfloor \frac{n}{k} \right \rfloor \right ) + \sum\limits_{m=1}^{q-1} \left ( S_j \left ( \left \lfloor \frac{n}{m} \right \rfloor \right ) - S_j \left ( \left \lfloor \frac{n}{m+1} \right \rfloor \right ) \right ) R_j(m)$$
The total complexity is $O(n^{3/4})$, but this can be easily improved to $O(n^{2/3})$ if we preprocess values smaller than $O(n^{2/3})$ with a sieve.
You should be able to calculate all of the values $\phi(1),\dots,\phi(N)$ simultaneously in time $O(N\log\log N)$, assuming you have sufficient memory.
To do so, set up a Sieve of Eratosthenes-type calculation, but instead of only recording whether every integer is prime or not, keep track of each step in the sieve that "crosses off" a given integer. The result is that you will have stored the list of all primes dividing $n$, for all $1\le n\le N$. (You can modify the sieve to get the complete factorization, but it's not important for this problem.)
Once you have this list in storage, you can calculate all the $\phi(n)$ by the formula $\phi(n)=n\prod_{p\mid n}(1-1/p)$. The total number of multiplications is $\sum_{n\le N} \omega(n)$, where $\omega(n)$ is the number of distinct prime factors of $n$; this sum is known to be $O(N\log\log N)$. (I'm sloppily counting a multiplication of two rational numbers as $1$ step.)
A similar setup will allow you to compute the values of any multiplicative function over an interval in time not much longer than the length of the interval.
spf (smallest prime factors) as a byproduct. Then: phi[1]=1; for i = 2 to N: {p = spf[i]; phi[i] = phi[i/p] * (p*p divides i ? p : p-1); }. Or something like that :-) But, as other answers have said; you don't need to compute all the phis to solve the original problem; it can be done in sublinear time.
– Don Hatch
Aug 23 '19 at 08:08
In the reply by plamenko to Andy above, we must be careful that R(n) is not the same as $R_0(n)$. I don't really understand why Andy didn't range his $(a,b)$ over $1\leq a\leq b\leq n$, instead of $a<b$. If he had, his proof would carry over just the same, and the summation would give $F(n)=S_1(n)=n(n+1)/2$.
The proof principle set up by Andy is valid for higher $j$, however, with plamenko's notation and [cond] returning 1 if cond is true and 0 otherwise, if you express $R_j(n)$ as $$R_j(n)=\sum_{1\leq a\leq b\leq n} [gcd(a,b)=1] b^j,$$ then you see that, by switching variables $a=mc,b=md$: $$R_j(\lfloor \frac nm\rfloor) = \sum_{1\leq c\leq d\leq \lfloor \frac nm\rfloor} [gcd(c,d)=1] d^j = \sum_{1\leq a\leq b\leq n} [gcd(a,b)=m] \frac{b^j}{m^j},$$ from which, summing over all $m$ like in Andy's proof, we get: $$\sum_{m=1}^n m^j R_j(\lfloor \frac nm\rfloor) = R_j(n) + \sum_{m=2}^n m^j R_j(\lfloor \frac nm\rfloor) = \sum_{m=1}^n \sum_{1\leq a\leq b\leq n} [gcd(a,b)=m] b^j = \sum_{1\leq a\leq b\leq n} b^j$$ which in the end resolves to $\sum_{1\leq b\leq n} b^{j+1} = S_{j+1}(n).$ So that proves plamenko's equation. The rest of plamenko's answer is unchanged, and very useful stuff indeed!
Actually I had a different idea. The number of elements in the Farey sequence of order $N$ is $1+\sum_{n=1}^N \phi(n)$. And one can recursively construct the entire Farey sequence in order (see the first displayed equation). So you might even be able to do this in time $O(N)$.