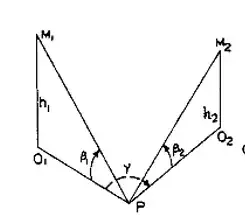
Given two points with 3D coordinates, and three angle observations, how to caculate the coordinate of the third point

Question

Given two points, $M_1(X_1,Y_1,Z_1)$ and $M_2(X_2,Y_2,Z_2)$,$P(X_p, Y_p,Z_p)$ is the unknown point. How to get the coordinates of $P$ by three angle observation .
The picture below displays the relationship between these points and observations.
$Q_1(X_1,Y_1,Z_p)$,$Q_2(X_2,Y_2,Z_p)$,$P(X_p, Y_p,Z_p)$ are on the horizontal plane $Z=Z_p$, the coords of $Q_1, Q_2$ means $M_1Q_1\bot Q_1P, M_2Q_2\bot Q_2P$. We have known three angle observations $\beta_1=\angle Q_1PM_1, \beta_2=\angle Q_2PM_2, \gamma=\angle Q_1PQ_2$. How to get $P(X_p, Y_p,Z_p)$?

I've tried to use vector vector angle formula to list three equations but it's hard to solve it. Can we denote $P(X_p, Y_p,Z_p)$ as $$X_p=f(X_1,Y_1,Z_1,X_2,Y_2,Z_2, \beta_1, \beta_2, \gamma)$$ $$Y_p=g(X_1,Y_1,Z_1,X_2,Y_2,Z_2, \beta_1, \beta_2, \gamma)$$ $$Z_p=u(X_1,Y_1,Z_1,X_2,Y_2,Z_2, \beta_1, \beta_2, \gamma)$$

Answer 1

Let $r_1=PQ_1$ and $r_2=PQ_2$. You have then two equations for the unknowns $r_1$, $r_2$: $$ r_1\tan\beta1-r_2\tan\beta_2=z_1-z_2; \quad r_1^2+r_2^2-2r_1r_2\cos\gamma=(x_1-x_2)^2+(y_1-y_2)^2. $$ You can solve and find $r_1$, $r_2$. You can then obtain the coordinates of $P$ from: $$ (x_p-x_1)^2+(y_p-y_1)^2=r_1^2; \quad (x_p-x_2)^2+(y_p-y_2)^2=r_2^2; \quad z_p=z_1-r_1\tan\beta_1. $$

Answer 2

Another possible approach would be as follows. You know that $P$ is on a downward opening cone with apex $M_1,$ axis $M_1Q_1,$ and half-opening angle $\frac\pi2 - \beta_1.$ It is also on a downward opening cone with apex $M_2,$ axis $M_2Q_2,$ and half-opening angle $\frac\pi2 - \beta_2.$

Finally, $P$ is on a cylinder with an axis parallel to the $z$ axis. To find the axis of the cylinder, you can find a circle in the $x,y$ plane that passes through $(X_1,Y_1,0)$ and $(X_2,Y_2,0)$ such that an inscribed angle on one of the arcs between those points is $\gamma.$ That means the two points $(X_1,Y_1,0)$ and $(X_2,Y_2,0)$ should subtend an angle of either $2\gamma$ or $\pi - 2\gamma$ from the center of the circle, depending on whether $\gamma$ is less than $\frac\pi2$ or greater.

If there are two possible circles, pick one. There will generally be two solutions and each circle would give one of them.

The equations of the two cones and the cylinder will give you three quadratic equations in three variables to solve.

Answer 3

Let $M_1(x_1,y_1,z_1),M_2(x_2,y_2,z_2),P(x,y,z)$. After transferring the origin to $M_1$ we get $M_1(0,0,0),M_2(x_2-x_1,y_2-y_1,z_2-z_1),P(x-x_1,y-y_1,z-z_1) $ or

$M_1(0,0,0),M_2(x_2,y_2,z_2),P(x,y,z)$ (say)

we have then $\cos\beta_{1} = \dfrac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+z^2}},\\ \cos\beta_{2} = \dfrac{\sqrt{{(x_2-x)}^2+{(y_2-y)}^2}} {\sqrt{{(x_2-x)}^2+{(y_2-y)}^2+{(z_2-z)}^2+}}\\ \cos\gamma = \dfrac{x^2+y^2-xx_2-yy_2}{\sqrt{{(x_2-x)}^2+{(y_2-y)}^2}\sqrt{{(x_2-x)}^2+{(y_2-y)}^2}}$

From above we get,

$x^2+y^2 = z^2\cot^2\beta_1\\ {(x-x_2)}^2+{(y-y_2)}^2 = ({z-z_2)}^2\cot^2\beta_2$

and using the last two eq. in $\cos\gamma$ we get

$z(z-z_2)\cos\gamma\cot\beta_1\cot\beta_2 = z^2\cot^2\beta_1 -xx_2-yy_2$

now $\cos\gamma\cot\beta_1\cot\beta_2 = k, \cot^2\beta_1=k_1, \cot^2\beta_2=k_2$ (let) we finally get

$x^2+y^2 = z^2k_1 --1\\ {(x-x_2)}^2+{(y-y_2)}^2 = ({z-z_2)}^2k_2 --2\\ xx_2+yy_2=z^2(k_1-k)+zz_2k --3$

after doing 1 -3 we get

$x(x-x_2) +y(y-y_2) = z^2k -zz_2k --4$

after doing 4-2 we get

$xx_2+yy_2= z^2(k-k_2)+zz_2(2k_2-k) - z_2^2k_2 +x_2^2+y_2^2 -- 5$

equating 3 and 5 we get

$z^2(k_1+k_2-2k) +z.2z_2(k-k_2)+z_2^2k_2 -(x_2^2+y_2^2) =0$

After getting values of z from here we easily get value of x and y from eq. 1 and 3.