Burgers equation with sinusoidal bump initial data

Question

Suppose we have $u_t + uu_x = 0 $ with

$$ \phi(x) = u(x,0) = \begin{cases} 0, && x \leq 0, x > 1 \\ \sin \pi x, && 0 < x \leq 1 \end{cases} $$

If we parametrize our curve with $\Gamma = (r,0,\phi(r) )$, then we know our characteristics are given by

$$ x(s) = \phi(r) s + r, \quad t(s) = s, \quad u(r,s) = \phi(r) $$

So, our solution is implicit

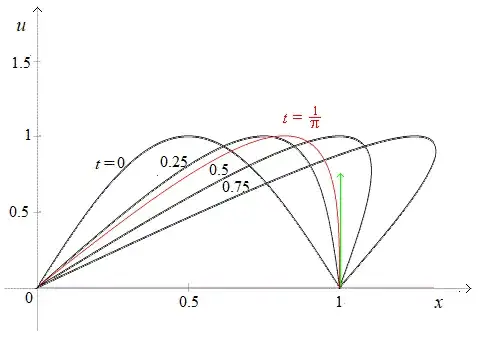
$$ u(x,t) = \phi(x - u t ) = \sin (x - ut ) \quad \text{when} \quad ut < x < ut + 1$$

The projected characteristics are given by

$$ x = \begin{cases} r, && r \leq 0, r > 1 \\ ( \sin \pi r ) t + r , && 0 < r \leq 1\end{cases}$$

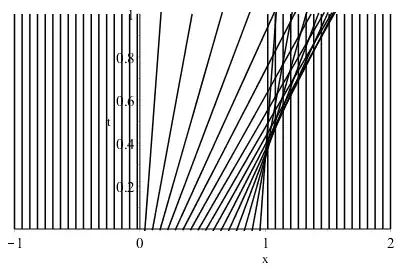
here I include the plots of the projected characteristics in the $t$-$x$ plane

Im having some dificulty to see from the my graph at what points will the solution become multivalued. From the graph it seems that it does when $t=0$ and $x=1$ because if you see at the graph the line with $r=0.9999$ will cross the vertical $x=1$. How can we find the weak solution of this pde?

Answer 1

Indeed, the characteristic curves $x = \phi(x_0) t + x_0$ along which $u = \phi(x_0)$ is constant are shown below:

Until characteristics intersect, the solution of the PDE is given by the method of characteristics, i.e. by solving $u = \phi(x-ut)$ numerically (I don't know any closed form expression). The breaking time $t_b$ where the solution becomes multi-valued can be computed as described in this post: $$ t_b = \frac{-1}{\inf \phi'} = \frac{1}{\pi} \approx 0.32 . $$ The speed of shock $\dot x_s$ satisfies the Rankine-Hugoniot condition $$ \dot x_s = \frac{1}{2}\big(\tilde u(x_s,t) + 0\big), \qquad x_s(1/\pi) = 1 $$ where $\tilde u(x_s,t)$ solves $\tilde u = \phi(x_s-\tilde ut)$. Hence, it is not easy to compute the shock trajectory $x_s(t)$ analytically in the present case. However, it is possible to derive some analytical expressions if the sinusoidal bump is replaced by a polynomial bump, e.g. the parabola $x\mapsto 4x(1-x)$ or the triangular function $x\mapsto 1-|2x-1|$ displayed below

Answer 2

This is more a comment than an answer, but not possible to edit with the figure in the comments section.

It is easier to see when the solution $u(x,t)$ becomes multivalued on the graph $u(x)$ at various $t$ than on the graph $x(t)$ at various $u$ :

Of course, the solution is on the form of implicit equation : $$u=\sin\left(\pi(x-t\,u) \right)$$ It is very easy to plot the above curves, without having $u(x,t)$ explicitly. The trick is explained in : plot solution that becomes multivalued

Plot the two branches : $\quad x(u)=\frac{1}{\pi}\sin^{-1}(u)+t\,u\quad$ and $\quad x(u)=\frac{1}{\pi}(\pi-\sin^{-1}(u))+t\,u$ .