plot solution that becomes multivalued

Question

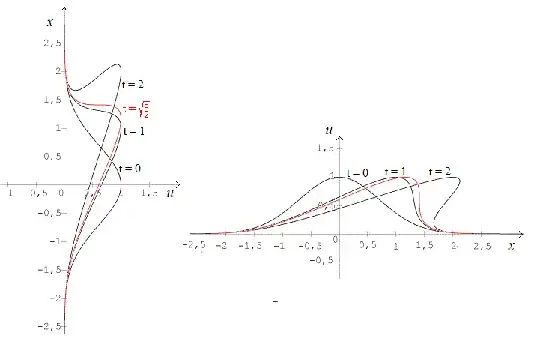
Consider burgers equations $u_t + u u_x =0 $ with initial data $u(x,0) = e^{-x^2}$. The characteristics are given by

$$ dx/ds = u, dt/ds = 1, du/ds = 0 $$

with initial curve $\Gamma = (r,0,e^{-r^2})$ So we have

$$ t = s, u = k $$

where $k$ is constant. and

$$ x = us + r $$ since $x(0)=r$. now since $u(x,t) = k = u(r,0) = e^{-r^2} = e^{-(x-ut)^2}$

So this is sol. Now, notice that when $t=0$ we obviously get our initial data $u(x,0) = e^{-x^2}$ and the characteristic line is $x= r $. Say now we increase $t=1$ we characteristic line $x=u+r$ and our solution becomes

$$ u(x,1) = e^{-(x-u(x,1)^2)} $$

how can we plot this?

Answer 1

I agree with your result : $$u(x,t) = e^{-(x-ut)^2}$$ This is an implicit equation. If you want explicitly $u(x,t)$ , then a special function is required, namely the Lambert W function.

If you only want to plot $u(x,t)$ , using the Lambert W function would be complicated, but possible.

There is a much simpler way. Plot $x(u,t)$ that is plot $x$ as a function of $u$ for various $t$. This is an explicit function : $$x(u,t)=t\,u\pm\sqrt{-\ln|u|}$$ Plot the two branches corresponding to the signs $+$ and $-$ successively.

With rotation/symmetry you get the wanted orientation of the figure. Or alternatively, directly plot $x$ as a function of $u$ on the inverted system of axes.

Note :The function $u(x,t)$ becomes to be multivalued at $t=\sqrt{\frac{e}{2}}$ (curve in red).

$\frac{du}{dx}=\infty$ at $\left(u=e^{-1/2} \:;\: x=\sqrt{2}\right)$.