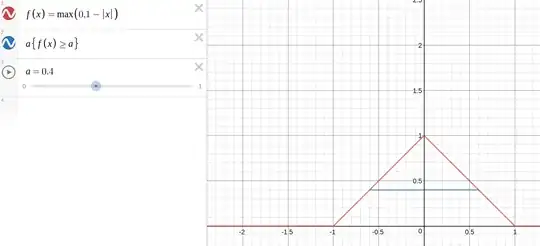
I'm having difficulty with this problem here:
Let $f\in L^1(X,\mathcal{M},\mu)$ with $||f||_1 \neq 0$.
Prove that there exists a unique $\alpha$ so that $ \mu(\lbrace|f|\geq \alpha\rbrace) = \frac{1}{\alpha} ||f||_1$.
My first thought was to use the Hardy LittleWood Maximal Theorem which says that there exists $C$ so that
$\mu(\lbrace Hf(x) >\alpha\rbrace) \leq \frac{C}{\alpha} ||f||_1$
Unfortunately this theorem does not take me very far in this approach.
Any help is appreciated.
Edit: It seems the question was asking to show that there is at most one such $\alpha$