15

[I corrected the pictures and deleted one question due to user i707107's valuable hint concerning cycles.]

Visualizing the functions $\mu_{n\ \mathsf{ mod }\ m}(k) = kn\ \ \mathsf{ mod }\ \ m$ as graphs reveals lots of facts of modular arithmetic, among others the fixed points of $\mu_{n\ \mathsf{ mod }\ m}$ and the fact that $\mu_{n\ \mathsf{ mod }\ m}$ acts as a permutation $\pi^n_m$ of $[m] = \{0,1,\dots,m-1\}$ iff $n$ and $m$ are coprime. Furthermore the cycle structure and spectrum of $\pi^n_m$ can be visualized and related to number theoretic facts about $n$ and $m$.

This is how the graph for $\mu_{3\ \mathsf{ mod }\ 64}(k) = 3k\ \ \mathsf{ mod }\ \ 64$ looks like when highlighting permutation cycles (the shorter the stronger):

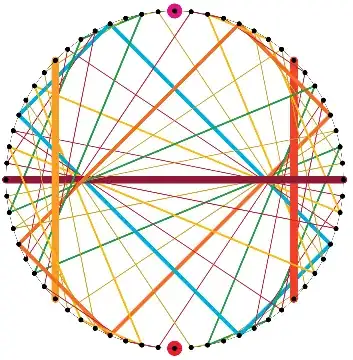
enter image description here

When visualizing the function $f^2_{\ \mathsf{ mod }\ m}(k) = k^2\ \ \mathsf{ mod }\ \ m$ (which gives the quadratic residue of $k$ modulo $m$) in the same way as a graph, other observations can be made and tried to relate to facts of number theory, esp. modular arithmetic:

enter image description here

These graphs are not as symmetric and regular than the graphs for $\mu_{n\ \mathsf{ mod }\ m}$ but observations can be made nevertheless:

  • the image of ${f^2_{\ \mathsf{ mod }\ m}}$, i.e. those $n$ with ${f^2_{\ \mathsf{ mod }\ m}}(k) = n$ for some $k < m$ (black dots)

  • number and distribution of fixed points with ${f^2_{\ \mathsf{ mod }\ m}}(k) = k$ (fat black dots)

  • cycles with ${f^2_{\ \mathsf{ mod }\ m}}^{(n)}(k) = k$ (colored lines)

  • parallel lines (not highlighted)

My questions are:

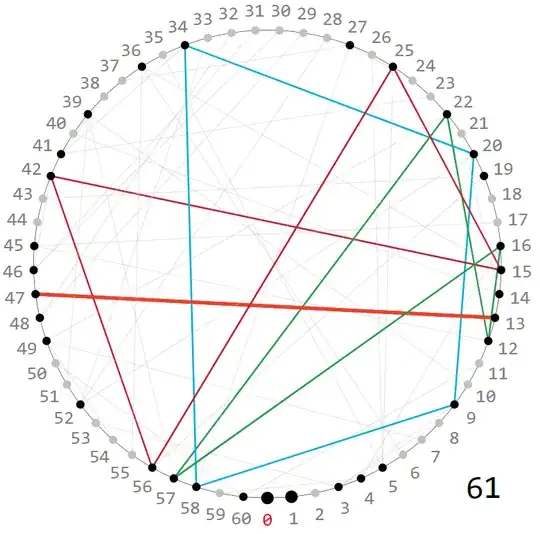
  • How can the symmetric distribution of image points $n$ (with $f^2_{\ \mathsf{ mod }\ 61}(k)=n$ for some $k$, black dots in the picture below) be explained?

  • Can there be more than one cycle of length greater than 1 for $f^2_{\ \mathsf{ mod }\ m}$?

  • How does the length of the cycles depend on $m$?

  • How does the "parallel structure" depend on $m$?

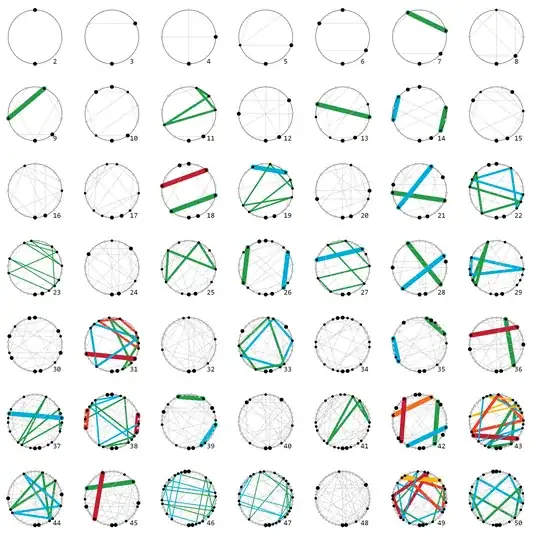
With "parallel structure" I mean the number and size of groups of parallel lines. For example, $f^2_{\ \mathsf{ mod }\ 8}$ has two groups of two parallel lines, $f^2_{\ \mathsf{ mod }\ 12}$ has two groups of three parallel lines. $f^2_{\ \mathsf{ mod }\ 9}$ has no parallel lines.

For $f^2_{\ \mathsf{ mod }\ 61}$ one finds at least four groups of at least two parallel lines:

enter image description here

For other prime numbers $m$ one finds no parallel lines at all, esp. for all primes $m\leq 11$ (for larger ones it is hard to tell).

Hans-Peter Stricker
  • 18,719
  • 3
    Use the CRT and the structure of $\mathbb{Z}/p^e\mathbb{Z}^\times$ to understand the multiplicative monoid of $\mathbb{Z}/m\mathbb{Z}$. You are supposed to start with the simplest case : $m$ odd prime, power of an odd prime, product of two primes (powers) – reuns Feb 14 '19 at 06:11
  • 2
    The parallelity has simple explanation. Obviously, the lines corresponding to $x\neq y$ are parallel if $x^2 + x = y^2 + y \pmod{m}$, which is equivalent to $x+y+1 = 0 \pmod{m}$. However, there can be no parallel lines visible if they collapse to a point (i.e $x^2 = x$) or coincide (when $x^2 = y, y^2 = x$). – zhoraster Feb 14 '19 at 12:14
  • 1
    E.g. for $m=5$, there is a suitable pair $(x,y) = (1,3)$, but $x^2 = x$, so no parallel lines. For $m=7$, there is a pair $(x,y) = (2,4)$, but $2^2 = 4$, $4^2 = 2$. For $m=11$, there are suitable pairs $(2,8)$, $(3,7)$, $(4,6)$, which are clearly visible. – zhoraster Feb 14 '19 at 12:21
  • 1
    By the way, for $m=9$, there are two pairs $(3,5)$ and $(2,6)$; why do you write there are none? – zhoraster Feb 14 '19 at 12:40
  • @zhoraster: Thanks for the hint. I've overseen them (having been "parallel blind") and removed the remark. – Hans-Peter Stricker Feb 14 '19 at 12:58
  • Can you make.black dots visible again for the last one ($m=61$) ? – Sungjin Kim Feb 14 '19 at 16:01
  • Unless I misunderstood to an extent this is handled here. Write $p-1=2^a m$ with $m$ odd. The multipicative group of residue classes modulo $p$ is reduced, after $a$ iterations of squaring, to a set (= a cyclic subgroup) of size $m$. From that point on squaring cyclically permutes the numbers within that subgroup of size $m$ the same way as doubling permutes the residue classes modulo $m$. Think: discrete logs are doubled in each iteration. – Jyrki Lahtonen Feb 15 '19 at 03:32
  • With $p=61$ we get $p-1=2^2\cdot15$, so after two squarings we are in a cyclic subgroup of order fifteen. Modulo $15$ doubling results in the cycles $$(0)(1248)(36C9)(5A)(7EDB).$$ Here $A=10,B=11$ etc. To reinterpret those cycles within you graph you need a primitive root $g$ modulo $61$. Those cycles occur within the subgroup generated by $g^4$ (four was the highest power of two dividing $p-1=60$). One cycle is thus $g^4\mapsto g^8\mapsto g^{16}\mapsto g^{32}\mapsto g^4$, as i707107 observed. – Jyrki Lahtonen Feb 15 '19 at 03:39
  • @i707107: Sorry that the black dots got lost. Now they are there again. – Hans-Peter Stricker Feb 15 '19 at 08:02

1 Answers1

7

This is not a complete answer to all of your questions. This is to show you some things you need to investigate. The first question is answered. The second question has an example. I do not know complete answers to the third and fourth questions, but I give a try on explaining your plot of $m=61$.

From your last sentences, it looks like you are interested in the case when $m$ is a prime. Let $m=p$ be an odd prime. Then consider $p\equiv 1$ mod $4$, and $p\equiv 3$ mod $4$.

In the former case $p\equiv 1$ mod $4$, we see the symmetric black dots. This is because the Legendre symbol at $-1$ is $1$. That is $$ \left( \frac{-1}p \right)=1. $$ This means $-1$ is a square of something in $\mathbb{Z}/p\mathbb{Z}$. Suppose $x\equiv y^2$ mod $p$, then we have $-x \equiv z^2$ mod $p$ for some $z\in\mathbb{Z}/p\mathbb{Z}$.

Your example $m=61$ is a prime that is $1$ mod $4$. Thus, we have a symmetric black dots.

In general when $p$ is an odd prime, the image of the square mapping is $$\{ x^2 \ \mathrm{mod} \ p| 0\leq x \leq \frac{p-1}2 \}.$$ Note that the black dots represent image of the square mapping.

Thus, the number of black dots is $\frac{p+1}2$. In your example of $m=61$, we have $31$ black dots.

Now we use a primitive root $g$ in $\mathbb{Z}/p\mathbb{Z}$. Then any element $x\in \mathbb{Z}/p\mathbb{Z} - \{0\}$, we have some integer $a$ such that $x\equiv g^a$ mod $p$. Then a cycle formed by square mapping which includes $x$ can be written as $$ \{g^{a\cdot 2^k} \ \mathrm{mod} \ p| k=0, 1, 2, \ldots \}. $$ To see if we have cycles, try solving $$ a\cdot 2^k \equiv a \ \mathrm{mod} \ p-1. $$

In your plot of $m=61$, we have a primitive root $g=10$ and the following are cycles of length greater than $1$. All of these should be considered with modulo $61$. $$ (g^{20} g^{40}), $$ $$ (g^4 g^8 g^{16} g^{32}), $$ $$ (g^{12} g^{24} g^{48} g^{36}), $$ $$ (g^{56} g^{52} g^{44} g^{28}) $$ I am not sure if you consider these as cycles, because there can be numbers in front of these, such as $$ g^5 \mapsto g^{10} \mapsto g^{20}, $$ and comes in to the cycle $(g^{20} g^{40})$.

Sungjin Kim
  • 20,850