1

In a parabola $y^2=4ax$ , the length of focal chord making an angle $\theta$ with the x - axis is $4acosec^2\theta$ . If a chord is drawn parallel to that focal chord which passes through vertex of parabola at (0,0) , it's length comes out to be $4acosec^2\theta cos\theta$ , it's quite easy to prove this using parametric coordinates for the parabola , I'm looking for an intuitive geometric demonstration that AB=A′B′.The equality certainly holds but I feel there must a visual way to show it.I have attached two geometrical 'viewpoints' from which i am seeing the scenario.enter image description hereenter image description here

Aditya Prakash
  • 592

2 Answers2

3

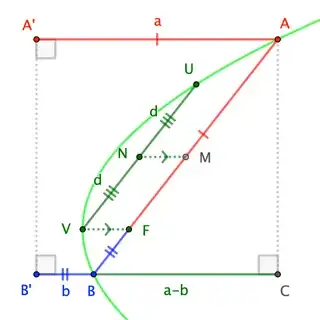
Changing the notation a bit, let $\overline{AB}$ be a chord through the parabola's focus, $F$, and let $\overline{UV}$ be a parallel chord through the vertex, $V$. Let $\overleftrightarrow{A^\prime B^\prime}$ be the parabola's directrix, and let $C$ be the fourth vertex of rectangle $\square AA^\prime B^\prime C$.

Writing $a := |AA^\prime| = |AF|$ and $b := |BB^\prime| = |BF|$ (and, without loss of generality, assuming $a\geq b$), we see that $|BC| = a-b$.

enter image description here

Now, recall that the midpoints of parallel chords of a parabola lie on a line parallel to the axis of that parabola. Consequently, if $M$ and $N$ are the midpoints of $\overline{AB}$ and $\overline{UV}$, respectively, then defining $d := |UN|=|VN|$, we have $$b + d = |BM| = \frac12|AB| = \frac12(a+b) \quad\to\quad d = \frac12(a-b) \quad\to\quad |UV| = |BC|$$

Blue
  • 83,939
2

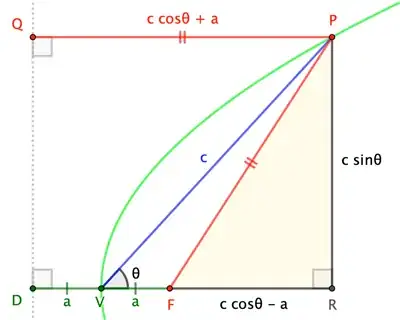
This isn't the approach you're taking, but it's pretty straightforward.

In the figure, $V$, $F$, and $\overleftrightarrow{DQ}$ are the the parabola's vertex, focus, and directrix. Recall that, by the defining property of the parabola, $|PF| = |PQ|$.

enter image description here

In $\triangle RPF$, $$|PR|^2 = \color{red}{|PF|^2} - |RF|^2 = \color{red}{|PQ|^2} - |RF|^2 = (|PQ|+|RF|)(|PQ|-|RF|)$$ $$c^2\sin^2\theta = 2 c\cos\theta \cdot 2a$$ $$c = 4a\cos\theta \csc^2\theta$$

Blue
  • 83,939
  • As I said , we can prove this with alternate ways but , I am not sure if I am putting this correctly , I was looking for a "cut and paste" kind of connection between AB and A'B' as marked in my diagram..the sort of visual proof we have Pythagoras theorem , I strongly feel there should be something. – Aditya Prakash Feb 03 '19 at 07:58
  • @ADITYAPRAKASH: Well, I acknowledged that this wasn't quite what you wanted; perhaps it might be helpful to others to see the length formula explicitly verified. That said, I believe I was a little confused by your question; I had interpreted it as looking to verify $AB=A'B'$ en route to showing the specific formula for the length of the vertex chord. I realize now that "all you want" is a geometric demonstration of the equality; the length formulas themselves are irrelevant, except insofar as they assure us that the equality is true. Is this correct? – Blue Feb 03 '19 at 08:28
  • Exactly , perfectly put. – Aditya Prakash Feb 03 '19 at 08:30
  • Then might I suggest rephrasing your question a bit? Display the image and write something like "I'm looking for an intuitive geometric demonstration that $AB=A'B'$. I happen to know (from analyzing a parameterization of the parabola) that the focal chord length is $4a\csc^2\theta$ and that $AB=4a\csc^2\theta\cos\theta$. So, the equality certainly holds, but I feel there should be a nice visual way to show it." – Blue Feb 03 '19 at 08:48