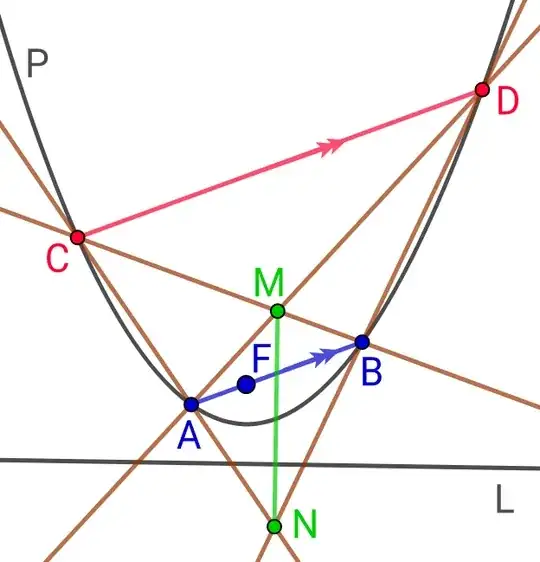
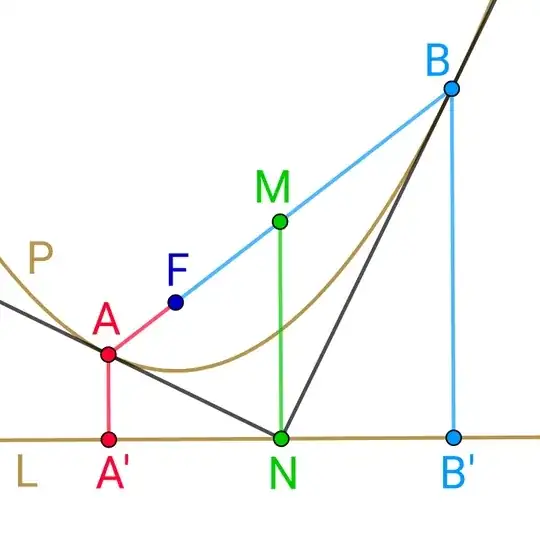
This answer shows the relation $CD=2MN$, but also gives some supplementary properties which may be useful in the context. (It is hard to build a hotel hall with walls in a parabola shape, but when we do so, knowing which distances are equal allow us to further use this information for further functional and esthetic architectural features.) All computations are typed in detail, there is no need for computer support.
Recall the midpoint theorem for conics, MT for short.
I will use the alternative notation $\Pi$ for the name of the given parabola, since $P$ is better suited for a point (after $M,N$ in the alphabet).
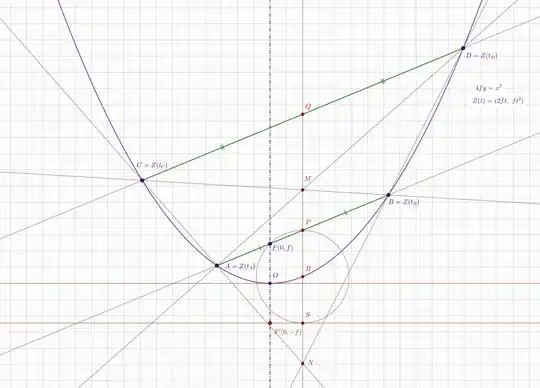
Below there will be also a simple analytic argument for MT. After a rotation we may assume that the given parabola has the $Oy$-axis as a symmetry axis, and its vertex is the origin $O(0,0)$. Let $f$ be the parameter that determines the focal point $F=(0,f)$. The directrix $(d)$ is then given by the equation $y=-f$.
We use the following parametrization for the parabola:
$$
Z(t) = (2ft,\ ft^2)\ .
$$
For points $A,B,C,\dots$ and so on on the parabola $\Pi$ we use the parameters (in notation) $t_A,t_B,t_C,\dots$ correspondingly.
First observation: For two points $C,D$ on $\Pi$ the slope of $CD$ is $\frac 12(t_C+t_D)$.
Proof: We compute this slope:
$$
\small
\frac{ft_C^2-ft_D^2}{2ft_C-2ft_D}
=
\frac{f(t_C-t_D)(t_C+t_D)}{2f(t_C-t_D)}
=
\frac 12(t_C+t_D)\ .
$$
Second observation, MT: If $A,B,C,D$ are arbitrary points on $\Pi$ so that $AB\|CD$ then the mid points of the segments $AB$, $CD$ are on the parallel to the $Oy$-axis with equation $x=f(t_A+t_B)=f(t_C+t_D)$.
Proof: It follows from the first observation, since the slopes are equal, $(t_A+t_B)/2=(t_C+t_D)/2$.
Third observation: Assume that $AB$ is a focal chord, i.e. $A,B\in\Pi$, $F\in AB$. Then $t_At_B=-1$.
Proof: We write the collinearity condition of $A,F,B$ using a determinant vanishing, then compute this determinant up to (simple, irrelevant) non-zero factors. When ignoring such a factor we write $\sim$ instead of $=$ sign.
$$
\small
0=
\begin{vmatrix}
1 & 0 & f\\
1 & 2ft_A & ft_A^2\\
1 & 2ft_B & ft_B^2
\end{vmatrix}
\sim
\begin{vmatrix}
1 & 0 & 1\\
1 & t_A & t_A^2\\
1 & t_B & t_B^2
\end{vmatrix}
=
\begin{vmatrix}
1 & 0 & 1\\
0 & t_A & t_A^2-1\\
0 & t_B & t_B^2-1
\end{vmatrix}
=
\begin{vmatrix}
t_A & t_A^2-1\\
t_B & t_B^2-1
\end{vmatrix}
\\
\sim(t_B-t_A)(t_At_B+1)
\sim(t_At_B+1)
\ .
$$
So we have $t_At_B=-1$.
$\square$
We consider now the situation from the given problem and introduce some auxiliary points:
Let $P,Q$ be the intersection points of the line $MN$ with $AB$, respectively $CD$. Then by the theorem of Ceva applied in the triangles $\Delta NAB$, $\Delta NCD$ and the cevians through $M$, and using Thales w.r.t. $AB\|CD$,
$$
\small
\begin{aligned}
-1 &= \frac{PA}{PB}\cdot\frac{DB}{DN}\cdot\frac{CN}{CA}= \frac{PA}{PB}\ ,\\
-1 &= \frac{QC}{QD}\cdot\frac{BD}{BN}\cdot\frac{AN}{AC}= \frac{QC}{QD}\ .\end{aligned}
$$
This shows that $P,Q$ are respectively the mid points of $AB$, $CD$.
By MT, the line $MNPQ$ is parallel to the symmetry axis of the given parabola $\Pi$. We intersect this line with the parabola $\Pi$ and with the directrix $d$:
- Let $R$ be $MNPQ\cap \Pi$.
- Let $S$ be $MNPA\cap d$.
Claim: The tangent $RR$ in $R$ to $\Pi$ is parallel to the direction $AB\|CD$. We have $RP=RS=RF$. We also have $RM=RN$. Finally:
$$
\bbox[lightgreen]{
\qquad
QC=QD=MN=2RM=2RN\ .
\qquad}
$$
Proof:
Consider instead of the segment $CD$ the limit segment in the same direction as $AB$ of length zero, so we consider the tangent parallel to $AB$ to $\Pi$. Let $R'$ be the tangency point. Then by MT the midpoint $R'$ of $R'R'$ is on the parallel to $Oy$ through $P$, so it is $R$.
The point $R$ has thus the $x$-coordinate same as $P$, so
$$
R= Z\left(\frac {t_A+t_B}2\right)
=\left(f(t_A+t_B),\ \frac 14f(t_A+t_B)^2\right)
\ .
$$
We compute its distance to $F,P,S$.
$$
\small
\begin{aligned}
F &= (0,f)\ ,\\
P &=\frac 12(A+B)=\frac 12(Z(t_A)+Z(t_B))=\left(f(t_A+t_B),\ \frac 12f(t_A^2+t_B^2)\right)\ ,\\
S &=(f(t_A+t_B), -f)\ ,\\[2mm]
R &=\left(f(t_A+t_B),\ \frac 14f(t_A+t_B)^2\right)
=\left(f(t_A+t_B),\ \frac 14f(t_A^2+t_B^2-2)\right)
\\
&=\frac 12(P+S)\ ,\qquad\text{ so $RP=RS=\frac 12PS$,}
\\[2mm]
PS&=y_P-y_S
=\frac 12f(t_A^2+t_B^2)-(-f)
=\frac 12f(t_A^2+t_B^2+2)
=\frac 12f(t_A^2+t_B^2-2t_At_B)
\\
&=\frac 12f(t_A-t_B)^2\ ,
\\[2mm]
RF^2 &= (f(t_A+t_B)-0)^2 + \left(\frac 14f(t_A+t_B)^2-f\right)^2
\\
&= f^2(t_A+t_B)^2 + f^2\left(\frac 14(t_A+t_B+2)(t_A+t_B-2)\right)^2
\\
&= \frac {f^2}{16}\Big(\ 16(t_A+t_B)^2 + (t_A+t_B+2)^2(t_A+t_B-2)^2\ \Big)^2
\\
&= \frac {f^2}{16}\Big(\ 16(t_A+t_B)^2 +
\big((t_A+t_B)^2+4(t_A+t_B)+4\big)
\big((t_A+t_B)^2-4(t_A+t_B)+4\big)
\ \Big)^2
\\
&= \frac {f^2}{16}\Big(\
\big((t_A+t_B)^2+4\big)^2
\ \Big)^2
\\
RF&=\frac f4\big((t_A+t_B)^2+4\big)^2=\frac f4\big((t_A-t_B)^2\big)^2=
\frac f4(t_A-t_B)^4=\frac 12PS=PR=RS\ .
\\[3mm]
\end{aligned}
$$
For the last part a similar computation is done.
For typing reasons i will use $t$ instead of $t_A$. Then $t_A=t$, $t_B=-\frac 1t=-\bar t$, and the $\bar t$-notation tries to avoid denominators. The line $MNPQ$ has thus the equation
$$x=f(t-\bar t)\ .$$
Because of $$2f(t_C+t_D)=2ft_C+2ft_D=x_C+x_D=2x_Q=2f(t-\bar t)\ $$
we may and will use a parametrization for $t_C,t_D$ as follows:
$$
\small
\begin{aligned}
t_C &=\frac 12(t-\bar t-u)\ ,\\
t_D &=\frac 12(t-\bar t+u)\ .
\end{aligned}
$$
We know $x_M=x_N=f(t-\bar t)$, so we only need $y_M,y_N$, and the distance $MN$ is the difference $y_M-y_N$. We compute $y_M=y_M(u)$ as the intersection $AD\cap MNPQ$, and $y_N=y_N(u)=y_M(-u)$ as $AC\cap MNPQ$. (Because $C$ is obtained from $D$ by replacing $u$ by $-u$.) Being on $AD$ the point $M=(f(t-\bar t),\ y_M)$ satisfies the relation:
$$
\small
\begin{aligned}
0 &=
\begin{vmatrix}
1 & f(t-\bar t) & y_M\\
1 & 2ft & ft^2\\
1 & f(t-\bar t+u) &\frac f4(t-\bar t+u)^2
\end{vmatrix}
\sim
\begin{vmatrix}
1 & t-\bar t & y_M\\
1 & 2t & ft^2\\
1 & t-\bar t+u &\frac f4(t-\bar t+u)^2
\end{vmatrix}
\\[2mm]
&=
\begin{vmatrix}
0 & -t-\bar t & y_M-ft^2\\
1 & 2t & ft^2\\
0 & -t-\bar t+u &\frac f4(t-\bar t+u)^2-ft^2
\end{vmatrix}
\sim
\begin{vmatrix}
t+\bar t & y_M-ft^2\\
t+\bar t-u &\frac f4(t-\bar t+u)^2-ft^2
\end{vmatrix}
\\[3mm]
&\qquad\text{ which gives}
\\[3mm]
y_M-ft^2 &=\frac {f(t+\bar t)}{4(t+\bar t-u)}
\Big((t-\bar t+u)^2-4t^2\Big)
\\
&=\frac {f(t+\bar t)}{4(t+\bar t-u)}
\Big((t-\bar t+u\ -2t)(t-\bar t+u\ +2t)\Big)
\\
&=-\frac {f(t+\bar t)}4 \cdot (3t-\bar t+u)
\ ,\\
y_N-ft^2 &=
-\frac {f(t+\bar t)}4 \cdot (3t-\bar t-u)
\ ,\\
y_M-y_N &=(y_M-ft^2 ) -(y_N-ft^2 )
\\
&=-\frac f2(t+\bar t)u\ .
\\[3mm]
&\qquad\text{ Also note that}
\\[3mm]
\frac 12(y_M+y_N)
&=
\frac 12(y_M-ft^2)
+
\frac 12(y_N-ft^2) + ft^2
=\frac f4\Big(4t^2-(t+\bar t)(3t-\bar t)\Big)
\\
&=
\frac f4\Big(t^2-2+\bar t^2\Big)
=\frac f4(t-\bar t)^2
=y_R\ ,
\quad\text{ so $R$ is the midpoint of $MN$. Finally:}
\\[3mm]
CD^2
&= (x_D-x_C)^2 + (y_D-y_C)^2
\\
&= (2ft_D-2ft_C)^2+(ft_D^2-ft_C^2)^2\\
&=4f^2(t_D-t_C)^2+f^2(t_D-t_C)^2(t_D+t_C)^2\\
&=4f^2u^2+f^2u^2(t-\bar t)^2=f^2u^2(t+\bar t)^2\\
&=4(y_M-y_N)^2\\
&=4MN^2\ .\\
\end{aligned}
$$
The last computation shows that we have
$$
CD = 2MN\ ,
$$
which is exactly the wanted relation.
$\square$
