Showing that $ |\cos x|+|\cos 2x|+\cdots+|\cos 2^nx|\geq \dfrac{n}{2\sqrt{2}}$

Question

For every nonnegative integer $n$ and every real number $ x$ prove the inequality:

$$\sum_{k=0}^n|\cos(2^kx)|= |\cos x|+|\cos 2x|+\cdots+|\cos 2^nx|\geq \dfrac{n}{2\sqrt{2}}$$

Answer 1

First an answer, then some interesting observations.

Lemma: For all $x$, we have $|\cos(x)| + |\cos(2x)| \geq 1/\sqrt{2}$.

Proof: The function $f(x) = |\cos(x)| + |\cos(2x)|$ obeys $f(x)=f(x+\pi)$ and $f(x) = f(-x)$. These symmetries let us reduce to verifying the claim for $x \in [0, \pi/2]$. We can split into considering the interval $[0, \pi/4]$, where $f(x) = \cos(x) + \cos(2x)$, and the interval $[\pi/4, \pi/2]$ where $f(x) = \cos(x) - \cos(2x)$. On both intervals, the second derivative is easily checked to be negative, so $f$ is concave down and the minima occur at the endpoints. We compute $f(0) =2$, $f(\pi/4) = 1/\sqrt{2}$ and $f(\pi/2) = 1$, so $f(\pi/4) = 1/\sqrt{2}$ is the minimum. $\square$

Now a proof: There are $n+1$ terms in the sum. Group them into consecutive pairs (possibly with one left over). There are $\lfloor (n+1)/2 \rfloor$ pairs. For each of them, the sum is greater than $1/\sqrt{2}$. So the sum is $\geq \lfloor (n+1)/2 \rfloor / \sqrt{2} \geq n/(2 \sqrt{2})$. $\square$.

---

Now, this is far from optimal. Set $$f(x) = \sum_{k=0}^n |\cos(2^k x) |.$$ As before, $f(x) = f(x + \pi) = f(-x)$, so we may restrict our attention to $x \in [0, \pi/2]$. Break this interval up into intervals of the form $I_j:=[j \pi/2^{n+1}, (j+1) \pi /2^{n+1}]$. On each interval $I_j$, the function $\cos(2^k x)$ has constant sign; let $\epsilon_{j,k}$ be $1$ or $-1$ according to the sign of $\cos(2^k x)$. So, on $I_j$, we have $$f(x) = \sum_{k=0}^n \epsilon_{j,k} \cos(2^k x)$$ $$f''(x) = - \sum_{k=0}^n 4^k \epsilon_{j,k} \cos(2^k x).$$ Since every term in the sum is positive, we see that $f$ is concave down on each interval $I_j$.

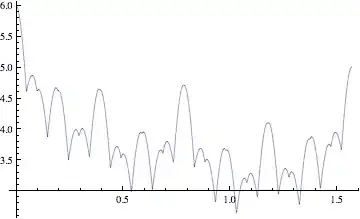
Here is a plot of $f(x)$ for $n=5$. So the minimum value of $f(x)$ is achieved an the endpoint of one of the intervals $I_j$, and must be achieved at a number of the form $j \pi/2^{n+1}$.

I set Mathematica to work finding these minima. Here is what I found: $$ \begin{array}{|r|ccccccccc|} \hline n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ \hline j & 1 & 3 & 5 & 11& 21 & 43 & 85 & 171 & 341 \\ j/2^{n+1} & 0.25 & 0.375 & 0.312 & 0.344 & 0.328 & 0.336 & 0.332 & 0.334 & 0.333 \\ \min f(x) /(n+1) & 0.354 & 0.363 & 0.411 & 0.423 & 0.438 & 0.446 & 0.453 & 0.458 & 0.463 \\ \hline \end{array} $$

I divide by $n+1$, not $n$, because it seems more natural to divide by the number of terms in the sum. In particular, by lumping more than $2$ terms together at once, we can improve on the bound of the problem. For example, lumping $4$ terms together proves $f(x) \geq 4 \lfloor (n+1)/4 \rfloor 0.411 \approx 0.411 n$ which (except for some very small values of $n$) beats $n/(2 \sqrt{2}) \approx 0.354 n$.

My guess is that $j/2^{n+1}$ is approaching $1/3$. At $x = \pi/3$, we have $f(x)/(n+1)$ equal to $1/2$. This data suggests that the true lower bound asymptotically is $n/2 - o(n)$, although the numerics suggest that it is approaching $1/2$ pretty slowly.

ADDED In fact, $j$ appears to always be the closest integer to $2^{n+1}/3$. It would be nice to have a rigorous proof of this.

Answer 2

We can use the following inequality:

$$|\cos x|\leq\tfrac12 \implies |\cos x|+|\cos 2x|\geq1.$$

Proof: use symmetry to reduce to the case $\cos x\in[\pi/3,\pi/2]$ where $\cos x-\cos 2x-1=(1-2\cos x)\cos x\geq 0.$

We can amortize the terms with $|\cos 2^kx|\leq \tfrac12$ by combining them with the next term, so every term effectively counts for $1/2$ except possibly the last. This gives the bound

$$\sum_{k=0}^n|\cos(2^kx)|= |\cos x|+|\cos 2x|+\cdots+|\cos 2^nx|\geq\frac n2.$$

Answer 3

Actually, the statement is true even when one restrict the sum to start at $k=1$.
i.e. For all $x \in \mathbb{R}$, $$\sum_{k=1}^n |\cos(2^k x)| \ge \frac{n}{2\sqrt{2}} \Leftrightarrow \varphi_n(2x) \ge 0$$ where $\varphi_n(x) = \sum_{k=0}^{n-1}|\cos(2^kx)| - \frac{n}{2\sqrt{2}}$. Notice:

$$\begin{align} \varphi_4(x) &= \varphi_2(x) + \varphi_2(4x)\\ \varphi_5(x) &= \varphi_2(x) + \varphi_3(4x)\\ &\,\,\vdots\\ \varphi_n(x) &= \varphi_2(x) + \varphi_{n-2}(4x) \end{align}$$

One only need to show $\varphi_2(x), \varphi_3(x) \ge 0$ for all $x$.

As other answer suggested, $|\cos(2^k x)|$ are piecewise concave functions. We have: $$\frac{d^2}{dx^2}|\cos(2^k x)| = -4^k |\cos(2^k x)| < 0 \,\,\,\text{ for } x \ne \pm 2^{-k}(l+\frac12)\pi \text{ where } l \in \mathbb{N} $$ This in turn implies $$\frac{d^2}{dx^2}\varphi_n(x) < 0 \,\,\,\text{ for } x \ne \pm2^{-n}(l+1)\pi \text{ where } l \in \mathbb{N}$$ The absolute minimum of $\varphi(x)$ must be located at a $x_{min}$ of the form $\pm 2^{-n}(l+1)\pi$.
Since $\varphi(x)$ is even and has period $\pi$, we only need to look for $x_{min}$ over the interval $[0, \frac{\pi}{2}]$.
For all x, we have:

$$\begin{align} \varphi_2(x) &\ge \min(\varphi_2(\frac{\pi}{4}),\varphi_2(\frac{\pi}{2})) = \varphi_2(\frac{\pi}{4}) = 0\\ \varphi_3(x) &\ge \min(\varphi_3(\frac{\pi}{8}), \varphi_3(\frac{\pi}{4}), \varphi_3(\frac{3\pi}{8}), \varphi_3(\frac{\pi}{2})) = \varphi_3(\frac{3\pi}{8}) = \cos(\frac{3\pi}{8}) - \frac{1}{2\sqrt{2}} > 0 \end{align}$$

Answer 4

This is terse and skips some important steps, but I speculate that it can be turned nicely into a clean proof!

We show: $$|\cos 2^n x | + |\cos 2^{n+1} x| \geq \frac{1}{\sqrt{2}}$$ We have $$ \sqrt{\cos^2 2^n x } + \sqrt{\cos^2 2^{n+1} x}. $$ And since $\cos^2 x = \frac{1}{2}(\cos(2x)+1)$ we get $$ \frac{1}{\sqrt{2}}\sqrt{\cos (2^{n+1} x) + 1} + \sqrt{\cos^2 (2^{n+1} x)}. $$ Substituting we get $$ \frac{1}{\sqrt 2}\sqrt{z+1}+ |z| $$ which has the minimum $\frac{1}{\sqrt 2}$ at $z=0$.

EDIT: Outline of complete proof

If $n$ is even, we are done since we have $n/2$ pairs. For $n$ is odd there might be a simple proof, but I couldn't come up with anything better than this.

We show $$|\cos 2^{n-1} x | + |\cos 2^n x | + |\cos 2^{n+1} x| \geq \frac{3}{2\sqrt{2}}$$ With tricks as above but also using $\cos(2x) = 2\cos^2(x) - 1$ on the last term we get $$\frac{1}{2}\sqrt{\cos 2^{n} x +1} + |\cos 2^n x | + |2\cos^2 2^{n} x-1| \geq \frac{3}{2\sqrt{2}}$$ and thus $$ \frac{1} {\sqrt 2}\sqrt{z+1}+ |z| + |2z^2-1| $$ which has minimum $$ \frac{\sqrt{2}+\sqrt{2-\sqrt{2}}}{2} > \frac{3}{2\sqrt{2}} $$ (Since wolframalpha told me so (difference 0.02913, hard one)).

Now we can use this inequality to get an even number of pairs. Anyone have a slicker proof for the odd case? This one sucks.

Answer 5

Hint: $$\large{|\cos x|+|\cos 2x|+\ldots+|\cos 2^nx|\geq n(\prod_{i=1}^n|\cos2^ix|)^\dfrac1n}$$ $$\large{n(\prod_{i=1}^n|\cos2^ix|)^\frac1n\ge n(|\cos x.\cos 2x.\ldots\cos 2^nx|^\dfrac1n=}$$$$\large{=n|\frac{(2\ sinx \cos x\cos 2x.\ldots\cos 2^nx)}{2sinx}^\dfrac1n|}$$=$$n|\frac{(\sin2x\cos 2x.\ldots\cos 2^nx)}{2sinx}^\dfrac1n|=....=$$$$=n(|\frac{sin2^{n+1}x}{2^n\ sinx}|)^\frac1n=\frac{n}{2}|\frac{sin2^{n+1}x}{sinx}|^\frac1n$$ that's enough to prove $$|\dfrac{\ sin2^{n+1}x}{\ sinx}|^\frac1n\ge\dfrac{1}{\sqrt2}$$ define $f(x)$ and show minimum of f is zero $f(x)= 2^\dfrac{n}{2}| sin2^{n+1}x|-|\ sinx|$