Two tangent circles are inscribed in a semicircle, one touching the diameter's midpoint; find the radius of the smaller circle

Question

I am unable to upload the image of my trials.

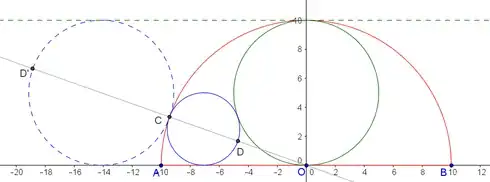
I assumed the radius of small circle is $x,$ horizontal distance between the centers of two circles is $y.$

I have joined the centers of the two circles and the length is $(5+x).$

I have drawn a vertical line from the center of the bigger circle to the center of the semi circle.

I have also drawn a horizontal line from the center of the small circle to the above line.

Then, by applying Pythagoras theorem, I get
$$(x+5)^2=(5-x)^2 + y^2.$$ I need one more equation to solve for $x.$

Intuitively I wonder if the radius of the small circle could be half of the big circle. I carefully constructed it and got $2.5 cm$ as the radius but I am not sure.

Answer 1

Let $R$ be the (known) radius of the large inscribed circle, $r$ the radius of the small inscribed circle, and $(x,r)$ the center of this small circle. Then one has the two equations $$x^2+(R-r)^2=(R+r)^2,\qquad\sqrt{x^2+r^2}+ r=2R$$ in the two unknowns $r$ and $x$.

Answer 2

In addition to using Pythagorean theorem, one can use circle inversion to figure out the radius of the small circle (let's call it $r$).

Let $AB$ be the base of the semicircle. Let $O$ be its midpoint. Let $C$ be the contact point between the small circle (blue) with the circular arc $AB$. Draw the line $OC$ and let $D$ be its other intersection with the small circle. $CD$ will be a diameter of the small circle.

Perform a circle inversion with respect to the circle centered at $O$ with radius $10$. The line $AB$ get mapped to itself. The big circle (green) get mapped to a line (green, dashed) parallel to $AB$ and at a distance $10$ from it. The small circle get mapped to a circle (blue, dashed) sandwiched between these two lines. So its diameter will be $10$. Let $D'$ be the image of $D$ under circle inversion. $CD'$ will be a diameter of the image of the small circle. We have

$$|CD'| = 10 \implies |OD'| = |OC|+|CD'| = 10 + 10 = 2|OC|$$ Circle invert $OD'$ back to $OD$, we find $$\begin{align}|OD| = \frac12|OC| &\implies |CD| = |OC| - |OD| = \frac12|OC|\\ &\implies r = \frac12|CD| = \frac14|OC| = \frac52 \end{align} $$ The radius we seek is $\frac52$. One half of that of the big circle and a quarter of that of the semicircle.

Answer 3

With hindsight - never any use, of course! - one can see that such a configuration must exist, because there exists an isosceles triangle whose sides are in the ratio of $3:2$ (whose height and angles one needn't know):

Answer 4

Let the radius of smaller circle be $\displaystyle r$ and x-coordinate of its center$\displaystyle ( C)$ is $\displaystyle a$. As the circle is touching x-axis, so the ordinate of center of cicle is equal to radius of the circle,i.e., $\displaystyle r$. Let the point of touching of semicircle and smaller circle be $\displaystyle P_{1}$ $\displaystyle ( x_{1}$$\displaystyle ,y_{1})$. As the semicircle and smaller circle touch each other so $\displaystyle P_{1}$, $\displaystyle C,Origin$ are collinear. \begin{gather*} \therefore \dfrac{r}{a} =\dfrac{y_{1}}{x_{1}} \ \ \ \ \ \ \ \ \ \ \ ( 1)\\ \end{gather*}

And the distance between $\displaystyle C$ and center of bigger circle is $\displaystyle r+5$ \begin{gather*} ( r-5)^{2} +a^{2} =( r+5)^{2}\\ or\ \ 20r=a^{2} \ \ \ \ \ \ \ \ \ \ ( 2) \end{gather*} Also the point $\displaystyle P_{1}$ satisfies both the semicircle and the smaller circle. \begin{gather*} \therefore x^{2}_{1} +y^{2}_{1} =100\ \ \ \ \ \ \ ( 3)\\ And\ ( x_{1} -a)^{2} +( y_{1} -r)^{2} =r^{2}\\ or\ x^{2}_{1} +y^{2}_{1} +a^{2} -2ax_{1} -2ry_{1} =0\\ or\ 100+a^{2} -2ax_{1} -2ry_{1} =0\ \ \ \ \ \ \ \ \ ( 4) \end{gather*} Solving these four equations, we get $\displaystyle r=2.5\ units$