0

If X is a binomial random variable, how do you find $E(X(X - 1)(X - 2))$? bab

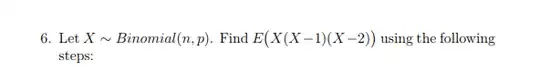
Here's my approach:

$E(X(X - 1)(X - 2)) = E(X^3 - 3X^2 + 2X)$

$E(X) = np, Var(X) = np(1 - p)$

$Var(X) = E(X^2) - (E(X))^2$

$E(X^2) = np(1 - p) + (np)^2$

So, $E(X^3 - 3X^2 + 2X) = E(X^3) - 3E(X^2) + 2E(X)$

How should I deal with $E(X^3)$?

Key Flex
  • 9,605
  • https://math.stackexchange.com/questions/1476676/the-3rd-raw-moment-of-a-binomial-distribution – 1123581321 Nov 21 '18 at 16:17
  • Analogue/Duplicate of this question from yesterday. Is it recent homework? (and Why did you leave the hint/"following steps" suggested out, incidentally?) – Clement C. Nov 21 '18 at 16:21

1 Answers1

0

Given any discrete random variable $X$, the probability generating function (pgf) of $X$ is $G_X(t):=\mathbb{E}t^X$. Note that $\mathbb{E}\prod_{i=0}^{n-1}(X-i)=G_X^{(n)}(1)$. As an example consider $X\sim B(n,\,p)\implies G_X(t)=\sum_{k=0}^\infty\binom{n}{k}(pt)^k q^{n-k}=(q+pt)^n$. Hence $\mathbb{E}X(X-1)(X-2)=n(n-1)(n-2)p^3(q+pt)^{n-3}|_{t=1}=n(n-1)(n-2)p^3$.

J.G.
  • 118,053